题目内容
12.某校高三(1)班32名学生参加跳远和掷实心球两项测试.跳远和掷实心球两项测试成绩合格的人数分别为26人和23人,这两项成绩均不合格的有3人,则这两项成绩均合格的人数是( )| A. | 23 | B. | 20 | C. | 21 | D. | 19 |
分析 设这两项成绩均合格的人数为x,根据集合关系建立方程进行求解即可.
解答  解:设这两项成绩均合格的人数为x,
解:设这两项成绩均合格的人数为x,
则跳远合格掷实心球不合格的人数为26-x,
则26-x+23+3=32,
得x=20,
即这两项成绩均合格的人数是20人,
故选:B
点评 本题主要考查集合关系的应用,建立Venn图表示集合关系是解决本题的关键.

练习册系列答案
相关题目
17.复数z满足(1+i)z=i+2,则z的虚部为( )
| A. | $\frac{3}{2}$ | B. | $\frac{1}{2}$ | C. | $-\frac{1}{2}$ | D. | $-\frac{1}{2}i$ |
4.函数f(x)=2x-sinx的图象大致是( )
| A. |  | B. |  | C. |  | D. |  |
1.双曲线$\frac{x^2}{16}-\frac{y^2}{9}=1$右焦点到渐近线的距离为( )
| A. | 3 | B. | 4 | C. | 5 | D. | $\frac{12}{5}$ |
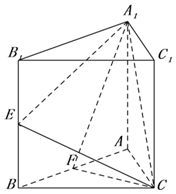 正三棱柱ABC-A1B1C1底边长为2,E,F分别为BB1,AB的中点.
正三棱柱ABC-A1B1C1底边长为2,E,F分别为BB1,AB的中点.