题目内容

设F是抛物线C1：y2=2pr（p＞0）的焦点，点A是抛物线C1与双曲线C2：
x2
a2
-
y2
b2
=1（a＞0，b＞0）的一条渐近线的一个公共点，且AF⊥x轴，则双曲线的离心率为
 
．
考点：双曲线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：求出抛物线的焦点坐标和准线方程，利用抛物线的定义得到
pb
2a
=
p
2
+
p
2
，利用离心率的定义求得双曲线的离心率．
解答： 解：由题意得F（
p
2
，0），准线为 x=-
p
2
，
设双曲线的一条渐近线为y=
b
a
x，则点A（
p
2
，
pb
2a
），
由抛物线的定义得|PF|等于点A到准线的距离，即
pb
2a
=
p
2
+
p
2
，
∴
b
2a
=1，
∴e=
c
a
=
1+(
b
a
)2
=
5
，
故答案为：
5
．
点评：本题考查抛物线的定义和双曲线、抛物线的标准方程，以及双曲线、抛物线的简单性质的应用，利用抛物线的定义 得到
pb
2a
=
p
2
+
p
2
，是解题的关键．
练习册系列答案
相关题目
已知向量
m
=（cos（x-
π
6
），0），
n
=（2，0），x∈R，函数f（x）=
m
•
n
．
（1）求函数f（x）的表达式；
（2）求f（π）的值；
（3）若f（α+
2π
3
）=
6
5
，α∈（-
π
2
，0），求f（2α）的值．
将自然1，2，3，4…排成数阵（如图），在2处转第一个弯，在3转第二个弯，在5转第三个弯，…．，则第20个转弯处的数为
 
．
已知向量
a
与
b
的夹角为60°，|
a
|=1，|
b
|=3，则|3
a
-
b
|=
 
．
如果执行如图所示的框图，输入N=5，则输出的数S=
 
已知|
a
|=2，|
b
|=3，＜
a
，
b
＞=60°，（
a
-
c
）•（
b
-
c
）=0，则|
c
|的最小值是
 
．
在2，3，6三个数中随机地抽取一个数记为a，再在剩余的两个数中随机地抽取一个数记为b，则“
a
b
是整数”的概率为
 
．
已知sinα-cosα=2sinαcosα，则sin2α=
 
．
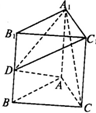如图，直三棱柱ABC-A1B1C1中，AB=AC=1，AA1=2，∠B1A1C1=90°，D为BB1的中点，则异面直线C1D与A1C所成角的余弦值为（　　）
A、
15
15
B、
2
5
7
C、
10
5
D、
10
15

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网