题目内容
设向量
与
的模分别为6和5，夹角为120°，则|
+
|等于 ．
| a |
| b |
| a |
| b |
考点：平面向量数量积的坐标表示、模、夹角
专题：平面向量及应用
分析：根据题意，利用平面向量的数量积求出模长即可．
解答：
解：根据题意，得；
|
|=6，|
|=5，
∴(
+
)2=
2+2
•
+
2=62+2×6×5cos120°+52=31，
∴|
+
|=
．
故答案为：
．
|
| a |
| b |
∴(
| a |
| b |
| a |
| a |
| b |
| b |
∴|
| a |
| b |
| 31 |
故答案为：
| 31 |
点评：本题考查了平面向量的应用问题，解题时应用平面向量的数量积求模长，是基础题．
练习册系列答案
相关题目
已知函数f（
）=
（x≠0，x≠1），且那么f（x）的解析式为（ ）
| 1 |
| x |
| 1 |
| x+1 |
A、
| ||
B、
| ||
C、
| ||
| D、1+x |
已知定义在R上的偶函数f（x）在区间[0，+∞）上是增函数，且f（1）=0，则不等式f（x）＜0的解集为（ ）
| A、（-1，1） |
| B、（-∞，-1）∪（1，+∞） |
| C、（-1，0） |
| D、（0，1） |
将四个数a=
，b=
，c=
，d=
从小到大排列是（ ）
| 3 | 2 |
| 3 | -2 |
| 1 | |||
|
| 3 | 4 |
| A、b＜a＜c＜d |
| B、b＜c＜d＜a |
| C、b＜c＜a＜d |
| D、a＜b＜c＜d |
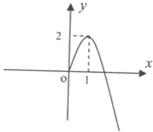已知奇函数f（x）在[0，+∞）上的图象是如图所示的抛物线的一部分．