题目内容
16．已知二次不等式ax2+2x+b＞0解集为{x|x≠-$\frac{1}{a}$}，则a2+b2-a-b的最小值为（ ）| A． | 0 | B． | 1 | C． | 2 | D． | 4 |
分析 根据一元二次不等式的解集得到a，b满足的条件，利用配方法结合基本不等式进行求解即可．
解答 解：∵二次不等式ax2+2x+b＞0解集为{x|x≠-$\frac{1}{a}$}，
∴$\left\{\begin{array}{l}{a＞0}\\{△=4-4ab=0}\\{-\frac{2}{2a}=-\frac{1}{a}}\end{array}\right.$，则a＞0且ab=1，
则a2+b2-a-b=（a+b）2-（a+b）-2ab=（a+b）2-（a+b）-2=（a+b-$\frac{1}{2}$）2-$\frac{9}{4}$，
∵a+b≥2$\sqrt{ab}$=2，∴当a+b=2时，a2+b2-a-b取得最小值此时a2+b2-a-b=22-2-2=0，
故选：A
点评 本题主要考查一元二次不等式以及基本不等式的应用，利用配方法和转化法是解决本题的关键．
练习册系列答案
相关题目
7．在物理实验中，为了研究所挂物体的重量x对弹簧长度y的影响．某学生通过实验测量得到物体的重量与弹簧长度的对比表：
（1）利用最小二乘法求y对x的回归直线方程；
（2）预测所挂物体重量为8g时的弹簧长度．
（参考公式及数据：$b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x•\overline y}}}{{\sum_{i=1}^n{x_i^2}-n{{\overline x}^2}}}，a=\overline y-b\overline x$，$\sum_{i=1}^5{{x_i}^2}=55$$\sum_{i=1}^5{{x_i}{y_i}}=72$）
| 物体重量（单位g） | 1 | 2 | 3 | 4 | 5 |
| 弹簧长度（单位cm） | 1.5 | 3 | 4 | 5 | 6.5 |
（2）预测所挂物体重量为8g时的弹簧长度．
（参考公式及数据：$b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x•\overline y}}}{{\sum_{i=1}^n{x_i^2}-n{{\overline x}^2}}}，a=\overline y-b\overline x$，$\sum_{i=1}^5{{x_i}^2}=55$$\sum_{i=1}^5{{x_i}{y_i}}=72$）
4．在棱锥P-ABC中，侧棱PA、PB、PC两两垂直，Q为底面△ABC内一点，若点Q到三个侧面的距离分别为3、4、5，则以线段PQ为直径的球的体积为（ ）
| A． | $\frac{125π}{6}$ | B． | $\frac{{125\sqrt{2}π}}{3}$ | C． | $\frac{50π}{3}$ | D． | $\frac{25π}{3}$ |
1．已知F1，F2为双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{16}$=1（a＞0）的左右焦点，点A在双曲线的右支上，点P（7，2）是平面内一定点，若对任意实数m，直线4x+3y+m=0与双曲线C至多有一个公共点，则|AP|+|AF2|的最小值为（ ）
| A． | 2$\sqrt{37}$-6 | B． | 10-3$\sqrt{5}$ | C． | 8-$\sqrt{37}$ | D． | 2$\sqrt{5}$-2 |
18．集合M={x|x2-x-6≥0}，集合N={x|-3≤x≤1}，则N∩（∁RM）等于（ ）
| A． | [-2，1] | B． | （-2，1] | C． | [-3，3） | D． | （-2，3） |
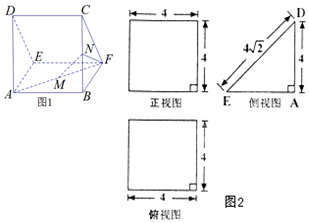一个多面体的直观图（图1）及三视图（图2）如图所示，其中M、N分别是AF、BC的中点，