Question

（Ⅰ）已知凸四边形ABCD，试比较AB•CD+BC•DA与AC•BD的大小．
（Ⅱ）△ABC三边a，b，c上的中线分别为m_a，m_b，m_c，求证：abm_c+bcm_a+cam_b≥a²m_a+b²m_b+c²m_c．

Answer 1

考点：不等式的证明,不等式比较大小

专题：证明题,不等式的解法及应用

分析：（Ⅰ）设A、B、C、D对应的复数分别为a、b、c、d，则 AB•CD+BC•DA=|a-b|•|c-d|+|b-c|•|a-d|=|（a-b）（c-d）|+|（b-c）（a-d）|，由复数模的性质：模的和不小于和的模，化简即可；
（Ⅱ）由（Ⅰ）的结论得，DG•CE+GE•CD≥CG•DE，即

1

3

m_a•

1

2

b+

1

3

m_b•

1

2

a≥

2

3

m_c•

1

2

c，化简即得bm_a+amb≥2cm_c，即有bcm_a+acm_b≥2c²m_c；同理得abm_c+bcm_a≥2b²m_b；abm_c+acm_b≥2a²m_a．累加即可得证．

解答： （Ⅰ）解：设A、B、C、D对应的复数分别为a、b、c、d，
则 AB•CD+BC•DA=|a-b|•|c-d|+|b-c|•|a-d|=|（a-b）（c-d）|+|（b-c）（a-d）|
≥|（a-b）（c-d）+（b-c）（a-d）|=|a-c|•|b-d|
即|a-b|•|c-d|+|b-c|•|a-d|≥|a-c|•|b-d|
∴AB•CD+BC•DA≥AC•BD．
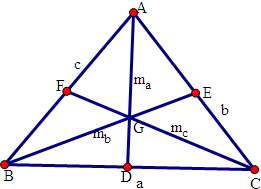
（Ⅱ）证明：如图，在四边形CDGE中，DE=

1

2

c，CG=

2

3

m_c，
CD=

1

2

a，CE=

1

2

b，DG=

1

3

m_a，EG=

1

3

m_b，
由（Ⅰ）的结论得，DG•CE+GE•CD≥CG•DE，即

1

3

m_a•

1

2

b+

1

3

m_b•

1

2

a≥

2

3

m_c•

1

2

c，
则有bm_a+amb≥2cm_c，即有bcm_a+acm_b≥2c²m_c；
同理可得am_c+cm_a≥2bm_b，即有abm_c+bcm_a≥2b²m_b；
bm_c+cm_b≥2am_a．即有abm_c+acm_b≥2a²m_a．
上面三式累加得，2bcm_a+2acm_b+2abm_c≥2a²m_a+2b²m_b+2c²m_c．
故abm_c+bcm_a+cam_b≥a²m_a+b²m_b+c²m_c．

点评：本题考查不等式的证明，以及不等式大小比较，考查综合法证明不等式，考查三角形的重心性质及中位线定理，是一道综合题．