题目内容
已知f（x）=|2x-1|+ax-5，如果函数y=f（x）恰有两个不同的零点，求a的值．
考点：函数零点的判定定理
专题：计算题,作图题,函数的性质及应用
分析：f（x）=|2x-1|+ax-5恰有两个不同的零点可化为函数y=|2x-1|与函数y=5-ax有两个不同的交点；作图求解．
解答：
解：f（x）=|2x-1|+ax-5恰有两个不同的零点可化为
函数y=|2x-1|与函数y=5-ax有两个不同的交点；
作函数y=|2x-1|与函数y=5-ax的图象如右图，
由图象可知，
当-2＜a＜2时，数y=|2x-1|与函数y=5-ax的图象有两个不同的交点，
即f（x）=|2x-1|+ax-5恰有两个不同的零点；
故-2＜a＜2．
解：f（x）=|2x-1|+ax-5恰有两个不同的零点可化为函数y=|2x-1|与函数y=5-ax有两个不同的交点；
作函数y=|2x-1|与函数y=5-ax的图象如右图，
由图象可知，
当-2＜a＜2时，数y=|2x-1|与函数y=5-ax的图象有两个不同的交点，
即f（x）=|2x-1|+ax-5恰有两个不同的零点；
故-2＜a＜2．
点评：本题考是了函数的零点与函数的图象的应用，同时考查了数形结合的思想应用，属于基础题．
练习册系列答案
相关题目
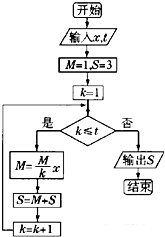执行如图所示的程序框图，如果输入x，t的值均为2，最后输出S的值为n，在区间[0，10]上随机选取一个数D，则D≤n的概率为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
已知x，y∈R，且2x+3y＞2-y+3-x，则下列各式中正确的是（ ）
| A、x-y＞0 |
| B、x+y＜0 |
| C、x-y＜0 |
| D、x+y＞0 |