题目内容
20.已知任意两个向量$\overrightarrow{a}$,$\overrightarrow{b}$,不等式|$\overrightarrow{a}$+$\overrightarrow{b}$|≤|$\overrightarrow{a}$|+|$\overrightarrow{b}$|是否正确?为什么?分析 可讨论向量$\overrightarrow{a},\overrightarrow{b}$是否共线,然后根据向量加法的三角形法则和平行四边形法则作出向量$\overrightarrow{a}+\overrightarrow{b}$,由图形即可判断$|\overrightarrow{a}+\overrightarrow{b}|$和$|\overrightarrow{a}|+|\overrightarrow{b}|$的大小关系,从而判断出不等式$|\overrightarrow{a}|+|\overrightarrow{b}|≤|\overrightarrow{a}|+|\overrightarrow{b}|$是否正确.
解答 解:(1)当向量$\overrightarrow{a},\overrightarrow{b}$共线,且方向相同时,$|\overrightarrow{a}+\overrightarrow{b}|=|\overrightarrow{a}|+|\overrightarrow{b}|$,如图所示:
(2)当向量$\overrightarrow{a},\overrightarrow{b}$共线,且方向相反时,$|\overrightarrow{a}+\overrightarrow{b}|<|\overrightarrow{a}|+|\overrightarrow{b}|$,如图所示: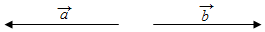
(3)当向量$\overrightarrow{a},\overrightarrow{b}$不共线时,设$\overrightarrow{OA}=\overrightarrow{a},\overrightarrow{OB}=\overrightarrow{b}$,如图,作$\overrightarrow{OC}=\overrightarrow{a}+\overrightarrow{b}$: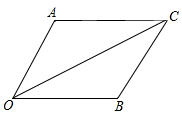
根据两边之和大于第三边得:$|\overrightarrow{a}+\overrightarrow{b}|<|\overrightarrow{a}|+|\overrightarrow{b}|$;
∴综上得,不等式$|\overrightarrow{a}+\overrightarrow{b}|≤|\overrightarrow{a}|+|\overrightarrow{b}|$正确.
点评 考查向量加法的三角形法则和平行四边形法则,以及三角形的两边之和大于第三边定理.

| A. | -1 | B. | 1 | C. | 0 | D. | 2 |
| A. | (x+2)2+(y+2)2=9 | B. | (x-2)2+(y+2)2=9 | C. | (x-2)2+(y-2)2=16 | D. | (x-2)2+(y+2)2=16 |