题目内容
12.已知过定点P(2,0)的直线l与曲线$y=\sqrt{2-{x^2}}$相交于A,B两点,O为坐标原点,当△AOB的面积最大时,直线l的倾斜角为( )| A. | 150° | B. | 135° | C. | 120° | D. | 30° |
分析 曲线y=$\sqrt{2-{x}^{2}}$为圆x2+y2=2的上半圆,由题意和三角形的面积公式可得当∠AOB=90°时,△AOB的面积取到最大值,O到直线l的距离OD=1,在直角三角形中由三角函数定义和倾斜角的定义可得.
解答 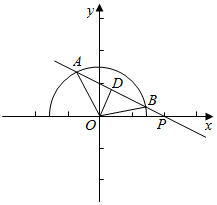 解:曲线y=$\sqrt{2-{x}^{2}}$为圆x2+y2=2的上半圆,
解:曲线y=$\sqrt{2-{x}^{2}}$为圆x2+y2=2的上半圆,
由题意可得△AOB的面积S=$\frac{1}{2}$•OA•OB•sin∠AOB=$\frac{1}{2}$•$\sqrt{2}$•$\sqrt{2}$•sin∠AOB=sin∠AOB,
当sin∠AOB=1即∠AOB=90°时,△AOB的面积取到最大值,
此时在RT△AOB中易得O到直线l的距离OD=1,
在RT△POD中,易得sin∠OPD=$\frac{OD}{OP}$=$\frac{1}{2}$,可得∠OPD=30°,
∴直线l的倾斜角为150°
故选:A
点评 本题考查直线与圆的位置关系,数形结合是解决问题的关键,属中档题.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
17.若在区间[0,π]上随机取一个数x,则sinx的值落在区间($\frac{1}{2}$,1)内的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{2}{π}$ |
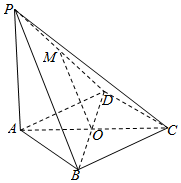 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,点O是对角线AC与BD的交点,AB=2,∠BAD=60°,M是PD的中点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,点O是对角线AC与BD的交点,AB=2,∠BAD=60°,M是PD的中点.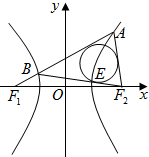 已知F1,F2是双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的左、右焦点,|F1F2|=4,点A在双曲线的右支上,线段AF1与双曲线左支相交于点B,△F2AB的内切圆与边BF2相切于点E.若|AF2|=2|BF1|,|BE|=2$\sqrt{2}$,则双曲线C的离心率为$\sqrt{2}$.
已知F1,F2是双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的左、右焦点,|F1F2|=4,点A在双曲线的右支上,线段AF1与双曲线左支相交于点B,△F2AB的内切圆与边BF2相切于点E.若|AF2|=2|BF1|,|BE|=2$\sqrt{2}$,则双曲线C的离心率为$\sqrt{2}$.