题目内容
集合A={x∈R|ax2-2x+1=0}的子集恰有两个,则实数a的集合为( )
| A、{a|a<1} |
| B、{a|a<1且a≠0} |
| C、{0,1} |
| D、{1} |
考点:子集与真子集
专题:集合
分析:对a分类讨论:当a=0时,当a≠0时,分别解出即可.
解答:
解:当a=0时,A={
},此时集合A只有两个子集:∅,{
},满足题意.
当a≠0时,∵集合A={x∈R|ax2-2x+1=0}的子集恰有两个,
∴ax2-2x+1=0有两个相等的实数根,∴△=0,∴4-4a=0,解得a=1.
此时A={1},满足题意.
综上可得:实数a的集合为{0,1}.
故选:C.
| 1 |
| 2 |
| 1 |
| 2 |
当a≠0时,∵集合A={x∈R|ax2-2x+1=0}的子集恰有两个,
∴ax2-2x+1=0有两个相等的实数根,∴△=0,∴4-4a=0,解得a=1.
此时A={1},满足题意.
综上可得:实数a的集合为{0,1}.
故选:C.
点评:本题考查了集合的性质、方程的实数根与判别式的关系、分类讨论的思想方法,属于基础题.

练习册系列答案
相关题目
下列函数中,满足“对任意的x1,x2∈R,当x1<x2时,都有f(x1)<f(x2)”的是( )
| A、y=log2x | ||
B、y=-
| ||
| C、y=2x | ||
| D、y=x2 |
圆锥的母线长为5,底面半径为3,则其体积为( )
| A、15π | B、30π |
| C、12π | D、36π |
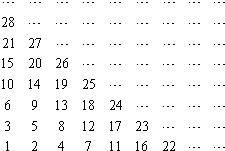 将自然数按如图排列,其中处于从左到右第m列从下到上第n行的数记为A(m,n),如A(3,1)=4,A(4,2)=12,则A(1,n)=
将自然数按如图排列,其中处于从左到右第m列从下到上第n行的数记为A(m,n),如A(3,1)=4,A(4,2)=12,则A(1,n)=