题目内容
已知:cosα=-
,α∈(π,
π),求sin(α+
)和cos(α-
)的值.
| 3 |
| 5 |
| 3 |
| 2 |
| π |
| 4 |
| π |
| 4 |
考点:两角和与差的正弦函数,两角和与差的余弦函数
专题:三角函数的求值
分析:根据题意和平方关系求出sinα的值,再由两角和的正弦(余弦)公式,求出sin(α+
)和cos(α-
)的值.
| π |
| 4 |
| π |
| 4 |
解答:
解:因为cosα=-
,α∈(π,
π),所以sinα=-
=-
,
则sin(α+
)=
sinα+
cosα=-
,
cos(α-
)=
cosα+
sinα=-
.
| 3 |
| 5 |
| 3 |
| 2 |
| 1-cos2α |
| 4 |
| 5 |
则sin(α+
| π |
| 4 |
| ||
| 2 |
| ||
| 2 |
7
| ||
| 10 |
cos(α-
| π |
| 4 |
| ||
| 2 |
| ||
| 2 |
7
| ||
| 10 |
点评:本题考查平方关系,以及两角和的正弦(余弦)公式的应用,注意三角函数值的符号.

练习册系列答案
相关题目
已知函数y=f(x)是定义域为R的偶函数.当x≥0时,f(x)=
若关于x的方程[f(x)]2+af(x)+b=0,a,b∈R有且仅有6个不同实数根,则实数a的取值范围是( )
|
A、(-
| ||||||
B、(-
| ||||||
C、(-
| ||||||
D、(-
|
已知log2m=2.013,log2n=1.013,则
等于( )
| n |
| m |
| A、2 | ||
B、
| ||
| C、10 | ||
D、
|
在锐角△ABC中,角A、B、C所对应的边分别为a,b,c,若b=2asinB,则角A等于( )
| A、30° | B、45° |
| C、60° | D、75° |
若a=40.9,b=80.48,c=(
)-1.5.a,b,c的大小是( )
| 1 |
| 2 |
| A、a>b>c |
| B、a<b<c |
| C、a<c<b |
| D、b<c<a |
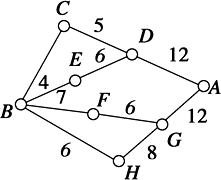 如图所示,小圆圈表示网络的结点,结点之间的连线表示它们有网线相联,连线标注的数字表示该段网线单位时间内可以通过的最大信息量,现从结点A向结点B传递信息,信息可以分开沿不同的路线同时传递,已知单位时间内传递的最大信息量为19,则从结点C向结点B单位时间内可以通过的最大信息量为
如图所示,小圆圈表示网络的结点,结点之间的连线表示它们有网线相联,连线标注的数字表示该段网线单位时间内可以通过的最大信息量,现从结点A向结点B传递信息,信息可以分开沿不同的路线同时传递,已知单位时间内传递的最大信息量为19,则从结点C向结点B单位时间内可以通过的最大信息量为