题目内容
14.某地区2007年至2013年居民人均纯收入y(单位:千元)的数据如表:| 年份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
| 年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(2)利用(1)中的回归方程,预测该地区2016年居民人均纯收入.
(参考公式:b=$\frac{\sum_{i=1}^{n}({t}_{i}-\overline{t})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({t}_{i}-\overline{t})^{2}}$,a=$\overline{y}$-b$\overline{t}$)
分析 (1)根据回归系数公式计算回归系数;(2)把x=10代入回归方程计算估计值.
解答 解:(1)∵$\overline t=\frac{1+2+…+7}{7}=4,\overline y=\frac{2.9+3.3+3.6+4.4+4.8+5.2+5.9}{7}=4.3$,
∴$b=\frac{3×1.4+2+0.7+0+0.5+1.8+4.8}{(9+4+1)×2}=\frac{14}{14×2}=\frac{1}{2}=0.5$,
$a=\overline y-b\overline t=4.3-\frac{1}{2}×4=2.3$;
(2)由(1)知y关于t的回归方程为y=0.5t+2.3.
当t=10时,y=0.5×10+2.3=7.3(千元),
答:预计到2016年,该区人均纯收入约7300元左右.
点评 本题考查了线性回归方程的求解和数值估计,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.已知:x=x1,x=x2是函数f(x)=$\frac{1}{3}$ax3-$\frac{1}{2}$ax2-x的两个极值点,且A(x1,$\frac{1}{{x}_{1}}$),B(x2,$\frac{1}{{x}_{2}}$),则直线AB与椭圆$\frac{{x}^{2}}{2}$+y2=1的位置关系为( )
| A. | 相切 | B. | 相交 | C. | 相离 | D. | 位置关系不正确 |
6.某几何体的三视图如图所示,则该几何体的体积为( )
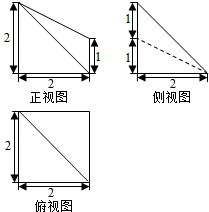

| A. | 8 | B. | $\frac{8}{3}$ | C. | $\frac{10}{3}$ | D. | $\frac{14}{3}$ |
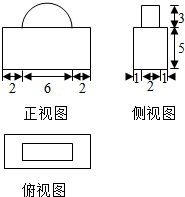 将一个长、宽、高分别为10、4、8的长方体毛坯加工成某工件,如图为加工后该工件的三视图,则该工件的材料利用率(材料利用率=$\frac{新工件的体积}{毛坯的体积}$)是$\frac{200+9π}{320}$.
将一个长、宽、高分别为10、4、8的长方体毛坯加工成某工件,如图为加工后该工件的三视图,则该工件的材料利用率(材料利用率=$\frac{新工件的体积}{毛坯的体积}$)是$\frac{200+9π}{320}$. 如图1,已知ABCD是上、下底边长分别为2和6的等腰梯形.将它沿对称轴OO1折成直二面角,如图2,满足AC⊥BO1.
如图1,已知ABCD是上、下底边长分别为2和6的等腰梯形.将它沿对称轴OO1折成直二面角,如图2,满足AC⊥BO1.