题目内容
18.函数f(x)=lnx-x2+4x+5的零点个数为( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 将函数的零点问题转化为方程的根的问题,利用数形结合进一步转化为函数图象的交点问题
解答  解:函数的定义域为(0,+∞),
解:函数的定义域为(0,+∞),
由f(x)=lnx-x2+4x+5=0,
得lnx=x2-4x-5=(x-2)2-9.
作出y=lnx和函数y=(x-2)2-9的图象,
由图象知两个函数有2个交点,
故f(x)=lnx-x2+4x+5有两个零点,
故选:C
点评 本题主要考查函数零点的关系,根据函数与方程之间的关系转化为两个函数的交点个数问题是解决本题的关键.函数的图象画法,考查数形结合的数学思想,正确作图是关键.

练习册系列答案
相关题目
9.已知:x=x1,x=x2是函数f(x)=$\frac{1}{3}$ax3-$\frac{1}{2}$ax2-x的两个极值点,且A(x1,$\frac{1}{{x}_{1}}$),B(x2,$\frac{1}{{x}_{2}}$),则直线AB与椭圆$\frac{{x}^{2}}{2}$+y2=1的位置关系为( )
| A. | 相切 | B. | 相交 | C. | 相离 | D. | 位置关系不正确 |
6.某几何体的三视图如图所示,则该几何体的体积为( )
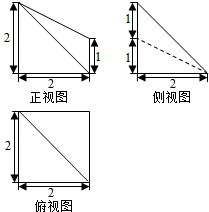

| A. | 8 | B. | $\frac{8}{3}$ | C. | $\frac{10}{3}$ | D. | $\frac{14}{3}$ |
13.已知全集M={-1,0,1,2,3,4},且A∪B={1,2,3,4},A={2,3},则B∩(∁MA)=( )
| A. | {1,4} | B. | {1} | C. | {4} | D. | ∅ |
8.在等比数列{an}中,已知a2•a6=16,则a4=( )
| A. | 4 | B. | -4 | C. | 8 | D. | ±4 |
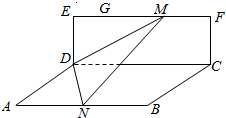 如图,矩形CDEF所在的平面与矩ABCD所在的平面垂直,AD=$\sqrt{2}$,DE=$\sqrt{3}$,AB=4,$\overrightarrow{EG}$=$\frac{1}{4}$$\overrightarrow{EF}$,点M在线段GF上(包括两端点),点N在线段AB上,且$\overrightarrow{GM}$=$\overrightarrow{AN}$,则二面角M-DN-B的平面角的取值范围为[$\frac{π}{4}$,$\frac{π}{3}$].
如图,矩形CDEF所在的平面与矩ABCD所在的平面垂直,AD=$\sqrt{2}$,DE=$\sqrt{3}$,AB=4,$\overrightarrow{EG}$=$\frac{1}{4}$$\overrightarrow{EF}$,点M在线段GF上(包括两端点),点N在线段AB上,且$\overrightarrow{GM}$=$\overrightarrow{AN}$,则二面角M-DN-B的平面角的取值范围为[$\frac{π}{4}$,$\frac{π}{3}$].