题目内容
已知数列{an}的前项n和为Sn,满足Sn=2an-2n(n∈N*).
(1)求数列{an}的通项公式an;
(2)若数列{bn}满足bn=
,Tn为数列{bn}的前项n和,求
Tn的值;
(3)数列{an}中是否存在三项ar,as,at(r<s<t)成等差数列?若存在.请求出一组适合条件的项;若不存在,说明理由.
(1)求数列{an}的通项公式an;
(2)若数列{bn}满足bn=
| 1 |
| an+2 |
| lim |
| n→∞ |
(3)数列{an}中是否存在三项ar,as,at(r<s<t)成等差数列?若存在.请求出一组适合条件的项;若不存在,说明理由.
考点:数列递推式
专题:等差数列与等比数列
分析:(1)由已知得{an+2}是首项为a1+2=4,公比为2的等比数列.由此能求出an=2n+1-2.
(2)bn=
=
=
,由此利用裂项求和法能求出Tn=
-
,从而得到
Tn=
(
-
)=
.
(3)假设存在这样3项,则有ar+at=2as,r<s<t,从而1+2t-r=2(s-r+1),由此推导出数列{an}中不存在三项ar,as,at(r<s<t)成等差数列.
(2)bn=
| 1 |
| an+2 |
| 1 |
| 2n+1-2+2 |
| 1 |
| 2n+1 |
| 1 |
| 2 |
| 1 |
| 2n+1 |
| lim |
| n→∞ |
| lim |
| n→∞ |
| 1 |
| 2 |
| 1 |
| 2n+1 |
| 1 |
| 2 |
(3)假设存在这样3项,则有ar+at=2as,r<s<t,从而1+2t-r=2(s-r+1),由此推导出数列{an}中不存在三项ar,as,at(r<s<t)成等差数列.
解答:
解:(1)a1=S1=2a1-2,a1=2.
an+1=Sn+1-Sn=2an+1-2-2an,
an+1=2an+2,
an+1+2=2(an+2),
{an+2}是首项为a1+2=4,公比为2的等比数列.
an+2=4•2n-1=2n+1,
an=2n+1-2.
(2)bn=
=
=
,
Tn=
+
+
+…+
=
=
-
,
∴
Tn=
(
-
)=
.
(3)假设存在这样3项,则有
ar+at=2as,r<s<t,
∴2r+1-2+2t+1-2=2(2s+1-2)
整理得到
2r+2t=2s+1,
两边同时除以2r,
1+2t-r=2(s-r+1),
等式左边为奇数+偶数,其结果必然为奇数,
等式右边为偶数,故上述等式不能成立,
∴数列{an}中不存在三项ar,as,at(r<s<t)成等差数列.
an+1=Sn+1-Sn=2an+1-2-2an,
an+1=2an+2,
an+1+2=2(an+2),
{an+2}是首项为a1+2=4,公比为2的等比数列.
an+2=4•2n-1=2n+1,
an=2n+1-2.
(2)bn=
| 1 |
| an+2 |
| 1 |
| 2n+1-2+2 |
| 1 |
| 2n+1 |
Tn=
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 16 |
| 1 |
| 2n+1 |
=
| ||||
1-
|
=
| 1 |
| 2 |
| 1 |
| 2n+1 |
∴
| lim |
| n→∞ |
| lim |
| n→∞ |
| 1 |
| 2 |
| 1 |
| 2n+1 |
| 1 |
| 2 |
(3)假设存在这样3项,则有
ar+at=2as,r<s<t,
∴2r+1-2+2t+1-2=2(2s+1-2)
整理得到
2r+2t=2s+1,
两边同时除以2r,
1+2t-r=2(s-r+1),
等式左边为奇数+偶数,其结果必然为奇数,
等式右边为偶数,故上述等式不能成立,
∴数列{an}中不存在三项ar,as,at(r<s<t)成等差数列.
点评:本题考查数列的通项公式的求法,考查数列的前n项和的极限值的求法,考查等差数列的判断与求法,解题时要认真审题,注意等比数列和等差数列的性质的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
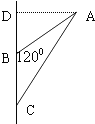 在△ABC中,AB=2,BC=1.5,∠ABC=120°(如图),若将△ABC绕直线BC旋转一周,则所形成的旋转体的体积是( )
在△ABC中,AB=2,BC=1.5,∠ABC=120°(如图),若将△ABC绕直线BC旋转一周,则所形成的旋转体的体积是( )A、
| ||
B、
| ||
C、
| ||
D、
|
函数y=3sin(2x+
)的一条对称轴方程为( )
| π |
| 3 |
A、x=
| ||
B、x=
| ||
C、x=
| ||
D、x=
|
在△ABC中,a2-c2+b2=-
ab,则角C=( )
| 3 |
| A、150° | B、60° |
| C、30° | D、45°或135° |
