题目内容
将正奇数按下表的规律填在5列的数表中,则第20行第3列的数字与第20行第2列数字的和为 .
| 1 | 3 | 5 | 7 | |
| 15 | 13 | 11 | 9 | |
| 17 | 19 | 21 | 23 | |
| 31 | 29 | 27 | 25 | |
| … | … | … | … | … |
考点:归纳推理
专题:推理和证明
分析:先观察第二、三、四列的数的排列规律,发现第三列数规律容易寻找,第三列数:3,11,19,27,…规律为8n-5,根据20×8-5=155,所以155应该出现在第20行第三列,又因为第20行的排列规律是偶数行,数是从大到小排列,所以得到结论
解答:
解:∵第三列数:3,11,19,27,…规律为8n-5,
∴根据20×8-5=155,所以155应该出现在第20行第三列
又因为第252行的排列规律是偶数行,数是从大到小排列奇数,
∴第20行第2列数字应为155+2=157,
第20行第3列的数字与第20行第2列数字的和为157+155=312
故答案为:312
∴根据20×8-5=155,所以155应该出现在第20行第三列
又因为第252行的排列规律是偶数行,数是从大到小排列奇数,
∴第20行第2列数字应为155+2=157,
第20行第3列的数字与第20行第2列数字的和为157+155=312
故答案为:312
点评:本题主要考查了数字的排列规律,找到相应行的规律是解决问题的关键,属于中档题.

练习册系列答案
相关题目
在极坐标系中,过点(2,
)且与极轴平行的直线方程是( )
| π |
| 2 |
| A、ρ=2 | ||
B、θ=
| ||
| C、ρcosθ=2 | ||
| D、ρsinθ=2 |
 已知三棱锥的底面是边长为2的正三角形,其正(主)视图与俯视图如图所示,则其侧(左)视图的面积为( )
已知三棱锥的底面是边长为2的正三角形,其正(主)视图与俯视图如图所示,则其侧(左)视图的面积为( )A、
| ||
B、
| ||
| C、3 | ||
D、2
|
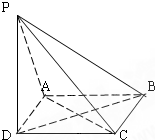 如图:已知四棱锥P-ABCD中,PD⊥平面ABCD,ABCD是正方形,PD=AD,
如图:已知四棱锥P-ABCD中,PD⊥平面ABCD,ABCD是正方形,PD=AD,