题目内容

13．已知f（x）=|x-a|+|x-1|
（Ⅰ）当a=2，求不等式f（x）＜4的解集；
（Ⅱ）若对任意的x，f（x）≥2恒成立，求a的取值范围．

分析 （Ⅰ）将a的值带入，通过讨论x的范围，求出不等式的解集即可；
（Ⅱ）根据绝对值的性质得到关于a的不等式，解出即可．

解答 解：（Ⅰ）当a=2时，不等式f（x）＜4，即|x-2|+|x-1|＜4，
可得$\left\{\begin{array}{l}{x≥2}\\{x-2+x-1＜4}\end{array}\right.$，或$\left\{\begin{array}{l}{1＜x＜2}\\{2-x+x-1＜4}\end{array}\right.$或$\left\{\begin{array}{l}{x≤1}\\{2-x+1-x＜4}\end{array}\right.$，
解得：-$\frac{1}{2}$＜x＜$\frac{7}{2}$，所以不等式的解集为{x|-$\frac{1}{2}$＜x＜$\frac{7}{2}$}．
（Ⅱ）∵|x-a|+|x-1|≥|a-1|，当且仅当（x-a）（x-1）≤0时等号成立，
由|a-1|≥2，得a≤-1或a≥3，
即a的取值范围为（-∞，-1]∪[3，+∞）．

点评 本题考查了解绝对值不等式问题，考查绝对值的性质，是一道基础题．

练习册系列答案
相关题目
3．已知$f（x）=\frac{lnx}{x}$，则（　　）
A．f（2）＞f（e）＞f（3）B．f（3）＞f（e）＞f（2）C．f（3）＞f（2）＞f（e）D．f（e）＞f（3）＞f（2）
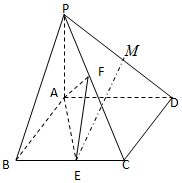4．已知四棱锥P-ABCD中，PA⊥平面ABCD，底面ABCD为菱形，∠ABC=60°，E是BC中点，M是PD上的中点，F是PC上的动点．
（Ⅰ）求证：平面AEF⊥平面PAD
（Ⅱ）直线EM与平面PAD所成角的正切值为$\frac{\sqrt{6}}{2}$，当F是PC中点时，求二面角C-AF-E的余弦值．
1．若定义在R上的函数f（x）满足f（x）+f'（x）＜1且f（0）=3，则不等式$f（x）＞\frac{2}{e^x}+1$（其中e为自然对数的底数）的解集为（-∞，0）．
8．△ABC的内角A，B，C的对边分别为a，b，c，已知a（sinA-sinB）=（c-b）（sinC+sinB）
（Ⅰ）求角C；
（Ⅱ）若c=$\sqrt{7}$，△ABC的面积为$\frac{3\sqrt{3}}{2}$，求△ABC的周长．
18．已知全集U={1，2，3，4，5，6，7}，集合A={1，3，7}，B={x|x=log2（a+1），a∈A}，则（∁UA）∩（
（∁UB）=（　　）
A．{1，3}B．{5，6}C．{4，5，6}D．{4，5，6，7}
5．在平面直角坐标系xOy中，将直线y=x与直线x=1及x轴所围成的图形绕x轴旋转一周得到一个圆锥，圆锥的体积V圆锥=${∫}_{0}^{1}$πx2dx=$\frac{π}{3}$x3|${\;}_{0}^{1}$=$\frac{π}{3}$．据此类比：将曲线y=2lnx与直线y=1及x轴、y轴所围成的图形绕y轴旋转一周得到一个旋转体，该旋转体的体积V=π（e-1）．
2．已知在平面直角坐标系xOy中，直线l的参数方程是$\left\{\begin{array}{l}x=\sqrt{2}•tsin\frac{π}{6}\\ y=tcos\frac{7π}{4}-6\sqrt{2}\end{array}\right.$（t是参数）
以原点O为极点，Ox为极轴建立极坐标系，圆C的极坐标方程为$ρ=4cos（{θ+\frac{π}{4}}）$．
（1）求直线l的普通方程和圆心C的直角坐标；
（2）求圆C上的点到直线l距离的最小值．
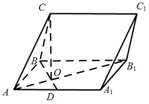3．在三棱柱ABCA1B1C1中，侧面ABB1A1为矩形，AB=3，AA1=3$\sqrt{2}$，D为AA1的中点，BD与AB1交于点O，CO⊥侧面ABB1A1．
（Ⅰ）证明：BC⊥AB1；
（Ⅱ）若OC=OA，求二面角A1-AC-B的余弦值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网