题目内容
5.在平面直角坐标系xOy中,将直线y=x与直线x=1及x轴所围成的图形绕x轴旋转一周得到一个圆锥,圆锥的体积V圆锥=${∫}_{0}^{1}$πx2dx=$\frac{π}{3}$x3|${\;}_{0}^{1}$=$\frac{π}{3}$.据此类比:将曲线y=2lnx与直线y=1及x轴、y轴所围成的图形绕y轴旋转一周得到一个旋转体,该旋转体的体积V=π(e-1).分析 根据类比推理,结合定积分的应用,即可求出旋转体的体积.
解答 解:由曲线y=2lnx,可得x=${e}^{\frac{y}{2}}$,
根据类比推理得体积V=${∫}_{0}^{1}π{e}^{y}$dy=$π{e}^{y}{|}_{0}^{1}$=π(e-1),
故答案为:π(e-1).
点评 本题主要考查旋转体的体积的计算,根据类比推理是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.已知角θ的顶点与原点重合,始边与x轴正半轴重合,终边在直线y=3x上,则sin(2θ+$\frac{π}{3}$)=( )
| A. | $\frac{3-4\sqrt{3}}{10}$ | B. | -$\frac{3-4\sqrt{3}}{10}$ | C. | $\frac{4-3\sqrt{3}}{10}$ | D. | -$\frac{4-3\sqrt{3}}{10}$ |
17.为了调查黄山市某校高中部学生是否愿意在寒假期间参加志愿者活动,现用简单随机抽样方法,从该校高中部抽取男生和女生共60人进行问卷调查,问卷结果统计如下:
(1)若用分层抽样的方法在愿意参加志愿者活动的学生抽取8人,则应从愿意参加志愿者活动的女生中抽取多少人?
(2)在(1)中抽取出的8人中任选3人,求被抽中的女生人数的分布列和数学期望.
| 是否愿意提供志愿者服务 性别 | 愿意 | 不愿意 |
| 男生 | 25 | 5 |
| 女生 | 15 | 15 |
(2)在(1)中抽取出的8人中任选3人,求被抽中的女生人数的分布列和数学期望.
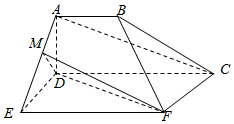 如图,空间几何体ADE-BCF中,四边形ABCD是梯形,四边形CDEF
如图,空间几何体ADE-BCF中,四边形ABCD是梯形,四边形CDEF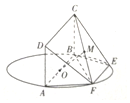 如图,AB为圆O的直径,点E,F在圆O上,AB∥EF,矩形ABCD所在的平面和圆(x-1)2+y2=1所在的平面互相垂直,且AB=2,AD=EF=1,∠BAF=60°.
如图,AB为圆O的直径,点E,F在圆O上,AB∥EF,矩形ABCD所在的平面和圆(x-1)2+y2=1所在的平面互相垂直,且AB=2,AD=EF=1,∠BAF=60°.