题目内容

5．某汽车销售公司同时在甲、乙两地销售一种品牌车，利润（单位：万元）分别为${L_1}=-{x^2}+21x$和L2=2x（其中销售量单位：辆）．若该公司在两地一共销售20辆，则能获得的最大利润为（　　）
A．130万元B．130.25万元C．120万元D．100万元

分析 由题意，设公司在甲地销售x辆（0≤x≤20，x为正整数），则在乙地销售（15-x）辆，公司获得利润L=-x2+21x+2（20-x），利用二次函数求最值即可．

解答 解：设甲地销售量为x辆，则乙地销售量为15-x 辆，获得的利润为L（x）万元，则
L（x）=-x2+21x+2（20-x）（0≤x≤20，x∈N+）
=-x2+19x+40，
所以，当x=9或或x=10时，利润最大，最大利润为130万元，
故选：A

点评 本题考查了学生将实际问题转化为数学问题的能力，属于中档题．

练习册系列答案
相关题目
15．已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）经过点M（2，0），离心率为$\frac{1}{2}$．A，B是椭圆C上两点，且直线OA，OB的斜率之积为-$\frac{3}{4}$，O为坐标原点．
（Ⅰ）求椭圆C的方程；
（Ⅱ）若射线OA上的点P满足|PO|=3|OA|，且PB与椭圆交于点Q，求$\frac{|BP|}{|BQ|}$的值．
16．如图，网络纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的体积为（　　）
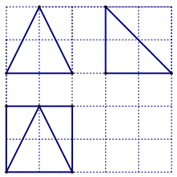
A．8B．$\frac{4}{3}$C．$\frac{8}{3}$D．$\frac{10}{3}$
13．已知f（x）=xlnx+mx，且曲线y=f（x）在点（1，f（1））处的切线斜率为1．
（1）求实数m的值；
（2）设$g（x）=f（x）-\frac{a}{2}{x^2}-x+a（{a∈R}）$在定义域内有两个不同的极值点x1，x2，求a的取值范围；
（3）已知λ＞0，在（2）的条件下，若不等式${e^{1+λ}}＜{x_1}•{x_2}^λ（{{x_1}＜{x_2}}）$恒成立，求λ的取值范围．
20．已知函数f（x）=x2-3mx+n（m＞0）的两个零点分别为1和2．
（1）求m、n的值；
（2）若不等式f（x）-k＞0在x∈[0，5]恒成立，求k的取值范围．
（3）令$g（x）=\frac{f（x）}{x}$，若函数F（x）=g（2x）-r2x在x∈[-1，1]上有零点，求实数r的取值范围．
10．把数列{2n+1}依次按一项、二项、三项、四项循环分为（3），（5，7），（9，11，13），（15，17，19，21），（23），（25，27），（29，31，33），（35，37，39，41），…在第100个括号内的最后一个数字为501．
17．若x，y满足约束条件$\left\{\begin{array}{l}x-y+1≥0\\ x+y-3≥0\\ x-3≤0\end{array}\right.$则z=x+2y的最小值为3．
4．实数x，y满足（x-y）2+y2=2，则x2+y2的最小值是3-$\sqrt{5}$，最大值是3+$\sqrt{5}$．
5．已知数列{an}满足a1=1，an+1-an=3n+2n+1求数列的通项公式．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网