Question

集合A={（x，y）|y=1-

4-x2

}，B={（x，y）|y=x+m}，若A∩B为单元素集，则m的取值范围为

 

．

Answer 1

考点：交集及其运算

专题：直线与圆

分析：根据方程y=1-

4-x2

得-1≤y≤1，并且该方程可变成x²+（y-1）²=4（-1≤y≤1），所以该方程表示以（0，1）为圆心，以2为半径的圆位于直线y=1下方的部分．而方程y=x+m表示斜率为1，在y轴上的截距为m的直线，由图象可以看出该直线的范围：在点（-2，1），（2，1）之间，所以将这两点带人直线方程即可求出m，从而求出m的范围．

解答： 解：由y=1-

4-x2

知0≤

4-x2

≤2，∴-2≤-

4-x2

≤0，-1≤1-

4-x2

≤1，即-1≤y≤1；
并且将该方程可变成：x²+（y-1）²=4（-1≤y≤1），∴该方程表示以（0，1）为圆心，2为半径的圆，并且是在y=1下方的部分；
y=x+m表示斜率为1，在y轴上的截距为m的直线，如下图所示：
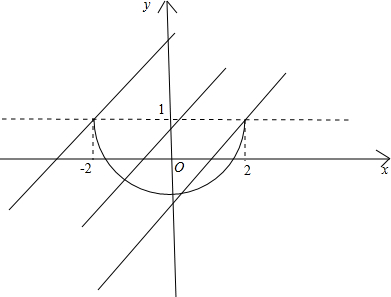若A∩B为单元素集，则直线和y=1下方的圆只有一个交点；
由图可以看出直线的范围在点（-2，1），（2，1）之间，并含点（-2，1），不含点（2，1）；
∴分别将点（-2，1），（2，1）带入直线方程得m=3，-1；
∴m的取值范围为（-1，3]．

点评：本题考查圆的方程，直线的方程，及交集为单元素集反应在图形上的含义，以及数形结合的方法．