题目内容

7．已知函数f（x）=|x-a|在（-∞，-1）上是单调函数，则a的取值范围是（　　）
A．（-∞，1]B．（-∞，-1]C．[-1，+∞）D．[1，+∞）

分析 根据绝对值函数的单调性进行求解即可．

解答 解：∵f（x）=|x-a|则（-∞，a]上为减函数，
∴若函数f（x）=|x-a|在（-∞，-1）上是单调函数，
则函数f（x）为减函数，此时满足a≥-1，
即实数a的取值范围是[-1，+∞），
故选：C．

点评 本题主要考查函数单调性的应用，根据绝对值函数的单调性是解决本题的关键．

练习册系列答案
相关题目
16．已知函数f（x）=$\left\{\begin{array}{l}{-2x，（-3≤x＜2）}\\{{2}^{x-1}，（2＜x≤3）}\end{array}\right.$，
（1）求函数f（x）的定义域和值域；
（2）作出函数f（x）的图象，并指出其单调区间．
18．已知两个向量$\overrightarrow{a}$，$\overrightarrow{b}$的夹角为30°，|$\overrightarrow{a}$|=$\sqrt{3}$，$\overrightarrow{b}$为单位向量，$\overrightarrow{c}$=t$\overrightarrow{a}$+（1-t）$\overrightarrow{b}$，则|$\overrightarrow{c}$|的最小值为$\frac{\sqrt{3}}{2}$．若$\overrightarrow{b}$•$\overrightarrow{c}$=0，则t=-2．
15．不等式2x-3y-5≥0表示的平面区域是（　　）
A．B．C．D．
2．设f（x）的定义域为A={x∈R|x≠0}，对任意的x，y∈A，都有f（x•y）=f（x）+f（y），且当x＞1时f（x）＞0．
（1）求f（1）和f（-1），并证明：$f（\frac{x}{y}）=f（x）-f（y）$；
（2）判断f（x）的奇偶性；
（3）证明：f（x）在区间（0，+∞）上是增函数．
12．已知△A1B1C1的三内角余弦值分别等于△A2B2C2三内角的正弦值，那么两个三角形六个内角中的最大值为钝角．
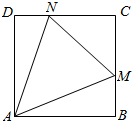19．如图，正方形ABCD的边长为2，M，N分别为边BC，CD上的动点，且∠MAN=45°，则$\overrightarrow{AM}•\overrightarrow{AN}$的最小值为8（$\sqrt{2}$-1）．
16．若正四面体ABCD的棱长为1，则它的外接球体积为（　　）
A．$\frac{\sqrt{6}}{8}$πB．$\frac{3}{2}$πC．$\frac{\sqrt{6}}{2}$πD．$\frac{\sqrt{3}}{4}$π
17．（Ⅰ）求过点（1，-1），且与直线x+4y-7=0垂直的直线方程．
（Ⅱ）求过点（1，-1），且与直线x+4y-7=0平行的直线方程．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网