题目内容
8.已知函数f(x)=$\frac{1}{x}$-log2x,在下列区间中,函数f(x)有零点的是( )| A. | (0,1) | B. | (1,2) | C. | (2,4) | D. | (4,+∞) |
分析 首先判断函数f(x)=$\frac{1}{x}$-log2x在(0,+∞)上是减函数,且连续;从而由零点的判定定理判断即可.
解答 解:易知函数f(x)=$\frac{1}{x}$-log2x在(0,+∞)上是减函数,且连续;
f(1)=1-0=1>0,f(2)=$\frac{1}{2}$-1=-$\frac{1}{2}$<0;
故函数f(x)有零点的区间是(1,2);
故选:B.
点评 本题考查了函数的性质的判断与应用及零点的判定定理的应用,注意掌握基本初等函数的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.若正四面体ABCD的棱长为1,则它的外接球体积为( )
| A. | $\frac{\sqrt{6}}{8}$π | B. | $\frac{3}{2}$π | C. | $\frac{\sqrt{6}}{2}$π | D. | $\frac{\sqrt{3}}{4}$π |
3.若集合A={x|lg(1-x)<0},集合B={x||x-1|<2},则A∩B=( )
| A. | (-1,0) | B. | (0,3) | C. | (-1,1) | D. | (0,1) |
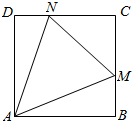 如图,正方形ABCD的边长为2,M,N分别为边BC,CD上的动点,且∠MAN=45°,则$\overrightarrow{AM}•\overrightarrow{AN}$的最小值为8($\sqrt{2}$-1).
如图,正方形ABCD的边长为2,M,N分别为边BC,CD上的动点,且∠MAN=45°,则$\overrightarrow{AM}•\overrightarrow{AN}$的最小值为8($\sqrt{2}$-1).