题目内容
12.设椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点F1、F2,其离心率e=$\frac{1}{2}$,且点F2到直线$\frac{x}{a}$+$\frac{y}{b}$=1的距离为$\frac{\sqrt{21}}{7}$.(1)求椭圆E的方程;
(2)设点P(x0,y0)是椭圆E上的一点(x0≥1),过点P作圆(x+1)2+y2=1的两条切线,切线与y轴交于A、B两点,求|AB|的取值范围.
分析 (1)设F1(-c,0),F2(c,0),依题意有$\frac{c}{a}=\frac{1}{2}$,$\frac{ab=bc}{\sqrt{{a}^{2}+{b}^{2}}}=\frac{\sqrt{21}}{7}$.可得c=1,a=2,b=$\sqrt{3}$,
(2)如图设圆的切线PM的方程为y=k(x-x0)+y0,由圆心(-1,0)到PM的距离为1,⇒|y0-k(x0+1)|=$\sqrt{1+{k}^{2}}$⇒(x02+2x0)k2-2y0(x0+1)k+y02-1=0,A(0,y0-kx0).设圆的切线PN的方程为y=k1(x-x0)+y0,同理可得B(0,y0-k1x0),依题意k1,k是方程(x02+2x0)k2-2y0(x0+1)k+y02-1=0的两个实根,|AB|2=[x0(k-k1)]2=$\frac{{{x}_{0}}^{2}(4{{y}_{0}}^{2}+4{{x}_{0}}^{2}+8{x}_{0})}{({{x}_{0}}^{2}+2{x}_{0})^{2}}$=$\frac{4{{y}_{0}}^{2}+4{{x}_{0}}^{2}++8{x}_{0}}{({x}_{0}+2)^{2}}$.由$3{{x}_{0}}^{2}+4{{y}_{0}}^{2}=12$,得|AB|2=1+$\frac{4({x}_{0}+2)}{({x}_{0}+2)^{2}}$=1+$\frac{4}{{x}_{0}+2}$.
解答 解:(1)设F1(-c,0),F2(c,0),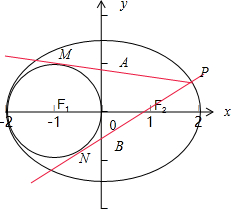
依题意有$\frac{c}{a}=\frac{1}{2}$,$\frac{ab=bc}{\sqrt{{a}^{2}+{b}^{2}}}=\frac{\sqrt{21}}{7}$.
又∵a2=b2+c2,∴c=1,a=2,b=$\sqrt{3}$,
∴椭圆E的方程为:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$.
(2)如图设圆的切线PM的方程为y=k(x-x0)+y0
由圆心(-1,0)到PM的距离为1,⇒
|y0-k(x0+1)|=$\sqrt{1+{k}^{2}}$⇒(x02+2x0)k2-2y0(x0+1)k+y02-1=0
令y=k(x-x0)+y0中x=0,y=y0-kx0
∴A(0,y0-kx0).
设圆的切线PN的方程为y=k1(x-x0)+y0.
同理可得B(0,y0-k1x0)
依题意k1,k是方程(x02+2x0)k2-2y0(x0+1)k+y02-1=0的两个实根,
k1+k=$\frac{2{y}_{0}({x}_{0}+1)}{{{x}_{0}}^{2}+2{x}_{0}}$,k1k=$\frac{{{y}_{0}}^{2}-1}{{{x}_{0}}^{2}+2{x}_{0}}$
|AB|2=[x0(k-k1)]2=$\frac{{{x}_{0}}^{2}(4{{y}_{0}}^{2}+4{{x}_{0}}^{2}+8{x}_{0})}{({{x}_{0}}^{2}+2{x}_{0})^{2}}$=$\frac{4{{y}_{0}}^{2}+4{{x}_{0}}^{2}++8{x}_{0}}{({x}_{0}+2)^{2}}$.
∵$3{{x}_{0}}^{2}+4{{y}_{0}}^{2}=12$,∴|AB|2=1+$\frac{4({x}_{0}+2)}{({x}_{0}+2)^{2}}$=1+$\frac{4}{{x}_{0}+2}$
∵1≤x0≤2,∴|AB|2=1+$\frac{4}{{x}_{0}+2}$$∈[2,\frac{7}{3}]$.
∴|AB|的取值范围为[$\sqrt{2},\frac{\sqrt{21}}{3}$]
点评 本题考查了椭圆的方程,椭圆与直线的位置关系,圆的切线问题,属于难题

| A. | -10 | B. | -11 | C. | -12 | D. | -16 |
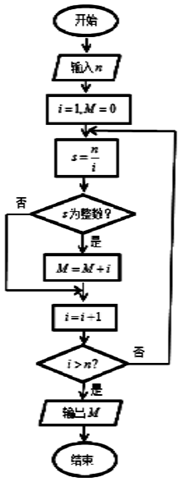 执行如图所示的程序框图,如果输入的n=32,那么输出的M=( )
执行如图所示的程序框图,如果输入的n=32,那么输出的M=( )| A. | 66 | B. | 65 | C. | 64 | D. | 63 |

| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
| A. | $\frac{π}{6}$ | B. | $\frac{5π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{3π}{4}$ |
 如图,已知△ABC内接于⊙O,连结AO并延长交⊙O于点D,∠ACB=∠ADC.
如图,已知△ABC内接于⊙O,连结AO并延长交⊙O于点D,∠ACB=∠ADC.