Question

已知函数.

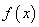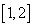（1）若在区间上不是单调函数，求实数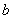的范围；

（2）若对任意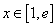，都有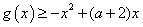恒成立，求实数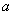的取值范围；

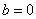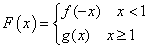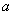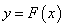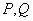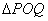（3）当时，设，对任意给定的正实数，曲线上是否存在两点，使得是以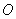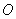（为坐标原点）为直角顶点的直角三角形，且此三角形斜边中点在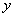轴上？请说明理由.

Answer 1

（1）由得，因在区间上不是单调函数.

所以在上最大值大于0，最小值小于0,

,

，.

(2)由，得,

，且等号不能同时取，，即.

恒成立，即.

令，求导得,

当时，，从而.

在上是增函数，.

.

(3)由条件，,

假设曲线上存在两点满足题意，则只能在轴两侧,

不妨设，则，且,

是以为直角顶点的直角三角形，,

    

是否存在等价于方程在且是否有解.

①当时，方程为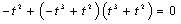，化简，此方程无解；

②当时，方程为，即

设，则,

显然，当时，，即在上为增函数.

的值域为，即，当时，方程总有解.

对任意给定的正实数，曲线上存在两点，使得是以（为坐标原点）为直角顶点的直角三角形，且此三角形斜边中点在轴上.