题目内容
已知两定点A(-1,0)和B(1,0),动点P(x,y)在直线l:y=x+2上移动,椭圆C以A,B为焦点且经过点P,则椭圆C的离心率的最大值为 .
考点:椭圆的简单性质
专题:直线与圆,圆锥曲线的定义、性质与方程
分析:作出直线y=x+2,过A作直线y=x+2的对称点C,2a=|PA|+|PB|≥|CD|+|DB|=|BC|,即可得到a的最大值,由于c=1,由离心率公式即可得到.
解答:
解: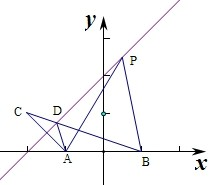 由题意知c=1,离心率e=
由题意知c=1,离心率e=
,
椭圆C以A,B为焦点且经过点P,
则c=1,
∵P在直线l:y=x+2上移动,
∴2a=|PA|+|PB|.
过A作直线y=x+2的对称点C,
设C(m,n),则由
,
解得
,即有C(-2,1),
则此时2a=|PA|+|PB|≥|CD|+|DB|=|BC|=
,
此时a有最小值
,
对应的离心率e有最大值
.
故答案为:
.
 由题意知c=1,离心率e=
由题意知c=1,离心率e=| c |
| a |
椭圆C以A,B为焦点且经过点P,
则c=1,
∵P在直线l:y=x+2上移动,
∴2a=|PA|+|PB|.
过A作直线y=x+2的对称点C,
设C(m,n),则由
|
解得
|
则此时2a=|PA|+|PB|≥|CD|+|DB|=|BC|=
| 10 |
此时a有最小值
| ||
| 2 |
对应的离心率e有最大值
| ||
| 5 |
故答案为:
| ||
| 5 |
点评:本题主要考查椭圆的定义和椭圆的离心率的求法,掌握直线的对称问题是解题的关键,属于中档题.

练习册系列答案
相关题目
圆锥的轴截面是等腰直角三角形,侧面积是16
π,则圆锥的体积是( )
| 2 |
A、
| ||
B、
| ||
| C、64π | ||
D、128
|
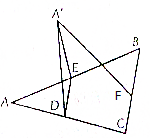 如图所示,在平面α内有一边长为a的等边△ABC,在△ABC中,DE∥BC,沿DE将△ABC折起,使它和△ABC所在半平面成60°的二面角,问直线DE取在何处,折起后的三角形顶点A(可记A′)到BC边的距离最短,最短距离是多少?
如图所示,在平面α内有一边长为a的等边△ABC,在△ABC中,DE∥BC,沿DE将△ABC折起,使它和△ABC所在半平面成60°的二面角,问直线DE取在何处,折起后的三角形顶点A(可记A′)到BC边的距离最短,最短距离是多少?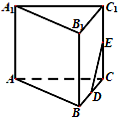 在如图所示的多面体中,四边形ABB1A1和ACC1A1都为矩形.AA1=1,AC=
在如图所示的多面体中,四边形ABB1A1和ACC1A1都为矩形.AA1=1,AC=