题目内容
14.已知椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左焦点为F(-c,0),离心率为$\frac{{\sqrt{3}}}{3}$,点M在椭圆上且位于第一象限,直线FM被圆x2+y2=$\frac{b^2}{4}$截得的线段的长为c,|FM|=$\frac{{4\sqrt{3}}}{3}$.(Ⅰ)求直线FM的斜率;
(Ⅱ)求椭圆的方程.
分析 (Ⅰ)由离心率为$\frac{{\sqrt{3}}}{3}$,得a2=3c2,b2=2c2,设直线FM的方程为y=k(x+c),由此利用已知条件能求出直线FM的斜率.
(Ⅱ)椭圆方程为$\frac{{x}^{2}}{3{c}^{2}}+\frac{{y}^{2}}{2{c}^{2}}=1$,直线FM的方程为y=$\frac{\sqrt{3}}{3}$(x+c),联立,消去y,得3x2+2cx-5c2=0,由此利用弦长公式能求出椭圆的方程.
解答 解:(Ⅰ)由离心率为$\frac{{\sqrt{3}}}{3}$,得$\frac{{c}^{2}}{{a}^{2}}=\frac{1}{3}$,又由a2=b2+c2,得a2=3c2,b2=2c2,
设直线FM的斜率为k(k>0),则直线FM的方程为y=k(x+c),
由已知有($\frac{kc}{\sqrt{{k}^{2}+1}}$)2+($\frac{c}{2}$)2=($\frac{b}{2}$)2,解得k=$\frac{\sqrt{3}}{3}$.
∴直线FM的斜率为$\frac{\sqrt{3}}{3}$.
(Ⅱ)由(Ⅰ)得椭圆方程为$\frac{{x}^{2}}{3{c}^{2}}+\frac{{y}^{2}}{2{c}^{2}}=1$,
直线FM的方程为y=$\frac{\sqrt{3}}{3}$(x+c),
两个方程联立,消去y,得3x2+2cx-5c2=0,
解得x=-$\frac{5}{3}c$或x=c,
∵点M在第一象限,∴M(c,$\frac{2\sqrt{3}}{3}c$),
由|FM|=$\sqrt{(c+c)^{2}+(\frac{2\sqrt{3}}{3}c-0)^{2}}$=$\frac{4\sqrt{3}}{3}$,解得c=1,
∴椭圆的方程为$\frac{{x}^{2}}{3}+\frac{{y}^{2}}{2}=1$.
点评 本题考查直线的斜率的求法,考查椭圆方程的求法,是中档题,解题时要认真审题,注意直线方程、椭圆性质、弦长公式的合理运用.

| A. | 10 | B. | 12 | C. | 5+3$\sqrt{2}$ | D. | 7+5$\sqrt{2}$ |
| A. | 若f1(-1)=f1(1),则f(-1)>f(1) | B. | 若f2(-1)=f2(1),则f(-1)>f(1) | ||
| C. | 若f(-1)=f(1),则f2(-1)>f2(1) | D. | 若f2(1)=f1(-1),则f1(-1)<f1(1) |
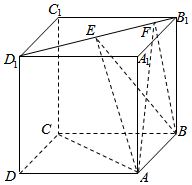 如图,正方体ABCD-A1B1C1D1的棱长为1,E,F是线段B1D1上的两个动点,且EF=$\frac{\sqrt{2}}{2}$,则下列结论中错误的是( )
如图,正方体ABCD-A1B1C1D1的棱长为1,E,F是线段B1D1上的两个动点,且EF=$\frac{\sqrt{2}}{2}$,则下列结论中错误的是( )| A. | AC⊥BF | B. | 三棱锥A-BEF的体积为定值 | ||
| C. | EF∥平面ABCD | D. | 面直线AE、BF所成的角为定值 |
| A. | $({\frac{11}{6},6}]$ | B. | $({\frac{11}{3},6})$ | C. | $({\frac{20}{3},\frac{26}{3}})$ | D. | $({\frac{20}{3},\frac{26}{3}}]$ |

 已知椭圆C:$\frac{x^2}{4}+{y^2}$=1,点M(x0,y0)是椭圆C上一点,圆M:(x-x0)2+(y-y0)2=r2.
已知椭圆C:$\frac{x^2}{4}+{y^2}$=1,点M(x0,y0)是椭圆C上一点,圆M:(x-x0)2+(y-y0)2=r2.