题目内容
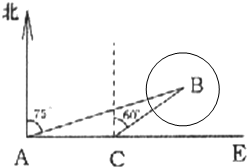如图，海中有一小岛B，周围3.8海里内有暗礁．一军舰从A地出发由西向东航行，望见小岛B在北偏东75°，航行8海里到达C处，望见小岛B在北偏东60°．（1）求C处与小岛B的距离BC．
（2）若此舰不改变舰行的方向继续前进，问此舰有没有角礁的危险？
考点：解三角形的实际应用
专题：应用题,解三角形
分析：（1）过B作AC的垂线垂足为D，令C点北向为F，由条件求得∠ACB=150°，∠ABC=15°，即可求出BC=8，
（2）在△BCD中，求得BD=4＞3.8，从而得出结论．
（2）在△BCD中，求得BD=4＞3.8，从而得出结论．
解答：
解：（1）过B点向AE作垂线，交AE于D，令C点北向为F．…（2分）
由题意可知：∠BAC=15°，∠ACF=90°，
∴∠ABC=180°-90°-60°-15°=15°，
∴BC=AC=8…（8分）
（2）在Rt△BCD中，∠BCD=30°，
=sin30°=
，BD=4，
∵BD=4＞3.8，此舰没有角礁的危险．…（14分）
解：（1）过B点向AE作垂线，交AE于D，令C点北向为F．…（2分）由题意可知：∠BAC=15°，∠ACF=90°，
∴∠ABC=180°-90°-60°-15°=15°，
∴BC=AC=8…（8分）
（2）在Rt△BCD中，∠BCD=30°，
| BD |
| BC |
| 1 |
| 2 |
∵BD=4＞3.8，此舰没有角礁的危险．…（14分）
点评：本题主要考查解三角形，直角三角形中的边角关系，属于中档题．
练习册系列答案
相关题目