题目内容
设数列{an}为等比数列,各项均为正数,且a2a6=4,则a1a2…a7= .
考点:等比数列的性质
专题:计算题,等差数列与等比数列
分析:利用等比数列通项的性质,即可得出结论.
解答:
解:∵数列{an}为等比数列,各项均为正数,且a2a6=4,
∴a4=2,
∵数列{an}为等比数列,
∴a1a2…a7=a47=27=128.
故答案为:128.
∴a4=2,
∵数列{an}为等比数列,
∴a1a2…a7=a47=27=128.
故答案为:128.
点评:本题主要考查了等比数列的性质的简单应用,属于基础试题

练习册系列答案
相关题目
向量
=(1,2),
=(1,-λ),在区间[-5,5]上随机取一个数λ,使向量2
+
与
-
的夹角为锐角的概率为( )
| a |
| b |
| a |
| b |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
若连续抛掷两次骰子得到的点数分别为m,n,m+n=5的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
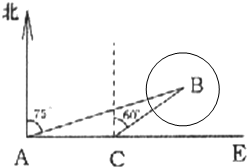 如图,海中有一小岛B,周围3.8海里内有暗礁.一军舰从A地出发由西向东航行,望见小岛B在北偏东75°,航行8海里到达C处,望见小岛B在北偏东60°.
如图,海中有一小岛B,周围3.8海里内有暗礁.一军舰从A地出发由西向东航行,望见小岛B在北偏东75°,航行8海里到达C处,望见小岛B在北偏东60°.