题目内容
已知函数f(x)满足:f(x1+x2)+f(x1-x2)=2f(x1)f(x2),且f(1)=
,求证:当n1<n2属于自然数时,f(n1)<f(n2)
| 3 |
| 2 |
考点:抽象函数及其应用
专题:函数的性质及应用
分析:根据关系式先计算出f(0)=1,要得到结论只需证明当n<n+1属于自然数时,f(n+1)-f(n)>0即可.
解答:
证明:根据题意,得f(1)+f(1)=2f(1)f(0),
又f(1)=
,所以f(0)=1.
对任意的实数t,因为f(t+1)+f(t-1)=2f(t)f(1)
=2f(t)×
=3f(t),
所以f(t+1)-f(t)=2f(t)-f(t-1)…(*)
又当x≥2时,f(
+
)+f(
-
)=2[f(
)]2,
即f(x)=2[f(
)]2-f(0)
=2[f(
)]2-1,
显然对任意的正整数x,都有f(x)恒大于零…(**).
下面用数学归纳法证明:当n<n+1属于自然数时,f(n+1)-f(n)>0
①当n=1时,f(1+1)=2[f(1)]2-f(0)=2×(
)2-1=
>
=f(1),
即f(2)-f(1)>0;
②假设n=k时成立,即f(k-1)<f(k).
则n=k+1时,由(*)及(**)可知
f(k+1)-f(k)=2f(k)-f(k-1)
>2[f(k)-f(k-1)]>0.
综上,当n1<n2属于自然数时,f(n1)<f(n2).
又f(1)=
| 3 |
| 2 |
对任意的实数t,因为f(t+1)+f(t-1)=2f(t)f(1)
=2f(t)×
| 3 |
| 2 |
=3f(t),
所以f(t+1)-f(t)=2f(t)-f(t-1)…(*)
又当x≥2时,f(
| x |
| 2 |
| x |
| 2 |
| x |
| 2 |
| x |
| 2 |
| x |
| 2 |
即f(x)=2[f(
| x |
| 2 |
=2[f(
| x |
| 2 |
显然对任意的正整数x,都有f(x)恒大于零…(**).
下面用数学归纳法证明:当n<n+1属于自然数时,f(n+1)-f(n)>0
①当n=1时,f(1+1)=2[f(1)]2-f(0)=2×(
| 3 |
| 2 |
| 7 |
| 2 |
| 3 |
| 2 |
即f(2)-f(1)>0;
②假设n=k时成立,即f(k-1)<f(k).
则n=k+1时,由(*)及(**)可知
f(k+1)-f(k)=2f(k)-f(k-1)
>2[f(k)-f(k-1)]>0.
综上,当n1<n2属于自然数时,f(n1)<f(n2).
点评:本题考查抽象函数表达式的意义和应用,灵活使用抽象函数的变形是解题的关键,属中档题.

练习册系列答案
相关题目
集合A={x∈Z|
<1},B={x∈N|lg(x-1)<
},从集合A,B中各取一个元素a,b,则a≠b的概率为( )
| 2x-1 |
| x-4 |
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
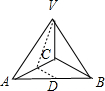 在三棱锥V-ABC中,D、E分别为AB,AC的中点,平面VCB⊥平面ABC,AC⊥BC.
在三棱锥V-ABC中,D、E分别为AB,AC的中点,平面VCB⊥平面ABC,AC⊥BC.