题目内容
设定义N*上的函数f(n)=
,an=f(1)+f(2)+f(3)+…+f(2n),那么an+1-an= .
|
考点:分段函数的应用
专题:计算题,函数的性质及应用,等差数列与等比数列
分析:由题意,得an+1=f(1)+f(2)+f(3)+…+f(2n)+f(2n+1)+…+f(2n+1),作差,得an+1-an,由函数解析式结合等差数列的求和公式计算可求得结果.
解答:
解:由函数f(n)=
,
an=f(1)+f(2)+f(3)+…+f(2n),得
an+1=f(1)+f(2)+f(3)+…+f(2n)+f(2n+1)+…+f(2n+1),
则有an+1-an=f(2n+1)+…+f(2n+1)
=(2n+1)+(2n-1+1)+(2n+3)+(2n-2+1)+(2n+5)+(2n-1+3)+…+1
=1+3+5+…+(2n+1)+…+(2n+1-1)=
(1+2n+1-1)•2n
=4n.
故答案为:4n.
|
an=f(1)+f(2)+f(3)+…+f(2n),得
an+1=f(1)+f(2)+f(3)+…+f(2n)+f(2n+1)+…+f(2n+1),
则有an+1-an=f(2n+1)+…+f(2n+1)
=(2n+1)+(2n-1+1)+(2n+3)+(2n-2+1)+(2n+5)+(2n-1+3)+…+1
=1+3+5+…+(2n+1)+…+(2n+1-1)=
| 1 |
| 2 |
=4n.
故答案为:4n.
点评:本题考查了分段函数与数列通项公式的综合应用,主要考查分段函数的意义和等差数列的求和公式,解题时要明确题目中函数解析式和数列通项公式表示的意义是什么.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
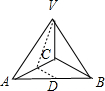 在三棱锥V-ABC中,D、E分别为AB,AC的中点,平面VCB⊥平面ABC,AC⊥BC.
在三棱锥V-ABC中,D、E分别为AB,AC的中点,平面VCB⊥平面ABC,AC⊥BC.