题目内容
某班级有3名学生被复旦大学自主招生录取后,大学提供了3个专业由这3名学生选择,每名学生只能选择一个专业,假设每名学生选择每个专业都是等可能的,则这3个专业中恰有一个专业没有学生选择的概率是 .
考点:计数原理的应用
专题:排列组合
分析:根据分类计数原理求出个专业中恰有一个专业没有学生选择的种数,再求出3个专业由这3名学生选择,每名学生只能选择一个专业的种数,最后利用古典概率求得.
解答:
解:这3个专业中恰有一个专业没有学生选择,第一步先从3名学生选出2个组成一个复合元素共有
种,再把这2个元素(包含一个复合元素)投放到3个专业中有
,
根据分步计数原理得这3个专业中恰有一个专业没有学生选择
=18,3个专业由这3名学生选择,每名学生只能选择一个专业有33=27种选法,
设事件A为“这3个专业中恰有一个专业没有学生选择”.
则P(A)=
=
.
故答案为:
.
| C | 2 3 |
| A | 2 3 |
根据分步计数原理得这3个专业中恰有一个专业没有学生选择
| C | 2 3 |
| •A | 2 3 |
设事件A为“这3个专业中恰有一个专业没有学生选择”.
则P(A)=
| 18 |
| 27 |
| 2 |
| 3 |
故答案为:
| 2 |
| 3 |
点评:本题主要考查了古典概率的求法以及排列组合中的混合问题,属于中档题.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目

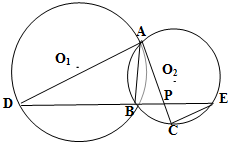 如图所示,已知⊙O1与⊙O2相交于A,B两点,过点A作⊙O1的切线交⊙O2于点C,过点B作两圆的割线,分别交⊙O1,⊙O2于点D,E,DE与AC相交于点P.若AD是⊙O2的切线,且PA=6,PC=2,BD=9,AB的长为
如图所示,已知⊙O1与⊙O2相交于A,B两点,过点A作⊙O1的切线交⊙O2于点C,过点B作两圆的割线,分别交⊙O1,⊙O2于点D,E,DE与AC相交于点P.若AD是⊙O2的切线,且PA=6,PC=2,BD=9,AB的长为