题目内容
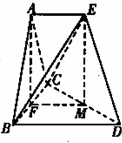
 如图,在几何体ABCDE中,平面ABC⊥平面BCD,AE∥BD,△ABC为边长等于2的正三角形,CD=2
如图,在几何体ABCDE中,平面ABC⊥平面BCD,AE∥BD,△ABC为边长等于2的正三角形,CD=2| 3 |
(Ⅰ)证明:平面ECD⊥平面ABC;
(Ⅱ)证明:EM∥平面ABC.
考点:平面与平面垂直的判定,直线与平面平行的判定
专题:证明题,空间位置关系与距离
分析:(Ⅰ)证明BC⊥CD,利用平面ABC⊥平面BCD,可得DC⊥平面ABC,即可证明平面ECD⊥平面ABC;
(Ⅱ)取BC中点F,连接FM,证明四边形AEMF为平行四边形,可得AF∥EM,即可证明:EM∥平面ABC.
(Ⅱ)取BC中点F,连接FM,证明四边形AEMF为平行四边形,可得AF∥EM,即可证明:EM∥平面ABC.
解答:
 证明:(Ⅰ)在△BCD中,BC=2,CD=2
证明:(Ⅰ)在△BCD中,BC=2,CD=2
,BD=4,
∴BC2+CD2=BD2,
∴BC⊥CD,
∵平面ABC⊥平面BCD,平面ABC∩平面BCD=BC,
∴DC⊥平面ABC,
∵DC?平面ECD,
∴平面ECD⊥平面ABC;
(Ⅱ)取BC中点F,连接FM.
在△BCD中,CF=FB=MD,
∴FM∥BD,FM=
BD,
∵AE=2,BD=4,AE∥BD,
∴FM∥AE.FM=AE,
∴四边形AEMF为平行四边形,
∴AF∥EM,
∵AF?平面ABC,EM?平面ABC,
∴EM∥平面ABC.
 证明:(Ⅰ)在△BCD中,BC=2,CD=2
证明:(Ⅰ)在△BCD中,BC=2,CD=2| 3 |
∴BC2+CD2=BD2,
∴BC⊥CD,
∵平面ABC⊥平面BCD,平面ABC∩平面BCD=BC,
∴DC⊥平面ABC,
∵DC?平面ECD,
∴平面ECD⊥平面ABC;
(Ⅱ)取BC中点F,连接FM.
在△BCD中,CF=FB=MD,
∴FM∥BD,FM=
| 1 |
| 2 |
∵AE=2,BD=4,AE∥BD,
∴FM∥AE.FM=AE,
∴四边形AEMF为平行四边形,
∴AF∥EM,
∵AF?平面ABC,EM?平面ABC,
∴EM∥平面ABC.
点评:本题考查平面与平面垂直的判定,考查直线与平面平行的判定,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
过原点的直线l与曲线C:
+y2=1相交,若直线l被曲线C所截得的线段长不大于
,则直线l的倾斜角α的取值范围是( )
| x2 |
| 3 |
| 6 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知0<k<
,则关于x的方程
=kx的实数解的个数是( )
| 1 |
| 3 |
| |2-x| |
| A、1个 | B、2个 | C、3个 | D、4个 |