题目内容
5.在区间[0,2]上分别任取两个数m,n,若向量$\overrightarrow{a}$=(m,n),$\overrightarrow{b}$=(1,1),则|$\overrightarrow{a}-\overrightarrow{b}$|≤1的概率是( )| A. | $\frac{π}{2}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{8}$ |
分析 由已知向量的坐标求出满足|$\overrightarrow{a}-\overrightarrow{b}$|≤1的m,n所满足的条件,结合m,n∈[0,2],数形结合得答案.
解答 解:由$\overrightarrow{a}$=(m,n),$\overrightarrow{b}$=(1,1),得$\overrightarrow{a}-\overrightarrow{b}=(m-1,n-1)$,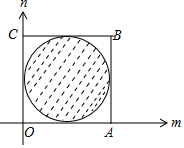
由|$\overrightarrow{a}-\overrightarrow{b}$|≤1,得$\sqrt{(m-1)^{2}+(n-1)^{2}}≤1$,即(m-1)2+(n-1)2≤1.
m,n满足$\left\{\begin{array}{l}{0≤m≤2}\\{0≤n≤2}\end{array}\right.$.
作出图形如图:
圆(m-1)2+(n-1)2=1的面积为π,正方形OABC的面积为4.
则|$\overrightarrow{a}-\overrightarrow{b}$|≤1的概率是$\frac{π}{4}$.
故选:B.
点评 本题考查几何概型,考查数学转化思想方法与数形结合的解题思想方法,是中档题.

练习册系列答案
相关题目
15.某人午觉醒来,打开收音机想听电台整点报时,则他等待不多于10分钟的概率是( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
16.执行如图所示的语句,结果为( )


| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
10.函数y=$\frac{{\sqrt{4-x}}}{x-1}$的定义域为( )
| A. | (-∞,4) | B. | (-∞,1)∪(1,4] | C. | (0,4) | D. | R |
17.“实数a、b、c不全为0“含义是( )
| A. | a、b、c均不为0 | B. | a、b、c中至少有一个为0 | ||
| C. | a、b、c中至多有一个为0 | D. | a、b、c中至少有一个不为0 |
14.下列推理正确的是( )
| A. | ∵a>b(a,b∈R),∴a+2i>b+2i(i是虚数单位) | |
| B. | 若f(x)是增函数,则f'(x)>0 | |
| C. | 若α,β是锐角△ABC的两个内角,则sinα>cosβ | |
| D. | 若A是△ABC的内角,且cosA>0,则△ABC为锐角三角形 |
15.要做一个圆锥形漏斗,其母线长为15cm,要使其体积最大,则其高应为( )
| A. | $10\sqrt{3}cm$ | B. | $8\sqrt{3}cm$ | C. | $6\sqrt{3}cm$ | D. | $5\sqrt{3}cm$ |