题目内容
已知函数f(x)是定义在(0,+∞)上的函数,对任意的x1,x2,当x1,x2(x1≠x2)都在(0,+∞)时总有(x1-x2)(f(x1)-f(x2))<0,并满足f(xy)=f(x)+f(y),f(
)=1.
(1)求f(1)的值;
(2)求证:f(x)在(0,+∞)上单调递减;
(3)如果f(x)+f(2-x)<2,求x的取值范围.
| 1 |
| 3 |
(1)求f(1)的值;
(2)求证:f(x)在(0,+∞)上单调递减;
(3)如果f(x)+f(2-x)<2,求x的取值范围.
考点:抽象函数及其应用
专题:计算题,证明题,函数的性质及应用,不等式的解法及应用
分析:(1)由f(xy)=f(x)+f(y),可令x=y=1,即可得到f(1);
(2)由于对任意的x1,x2,当x1,x2(x1≠x2)都在(0,+∞)时,总有(x1-x2)(f(x1)-f(x2))<0,即x1<x2时,总有f(x1)>f(x2)成立,由单调性的定义,即可得证;
(3)由于f(xy)=f(x)+f(y),f(
)=1.则f(
)=2f(
)=2.再由函数的单调性,即可解出不等式
f(x)+f(2-x)<2,注意定义域.
(2)由于对任意的x1,x2,当x1,x2(x1≠x2)都在(0,+∞)时,总有(x1-x2)(f(x1)-f(x2))<0,即x1<x2时,总有f(x1)>f(x2)成立,由单调性的定义,即可得证;
(3)由于f(xy)=f(x)+f(y),f(
| 1 |
| 3 |
| 1 |
| 9 |
| 1 |
| 3 |
f(x)+f(2-x)<2,注意定义域.
解答:
(1)解:由f(xy)=f(x)+f(y),
可令x=y=1,则f(1)=f(1)+f(1),
即有f(1)=0;
(2)证明:由于对任意的x1,x2,当x1,x2(x1≠x2)都在(0,+∞)时,
总有(x1-x2)(f(x1)-f(x2))<0,
即x1<x2时,总有f(x1)>f(x2)成立,
则f(x)在(0,+∞)上单调递减;
(3)解:由于f(xy)=f(x)+f(y),f(
)=1.
则f(
)=2f(
)=2.
则f(x)+f(2-x)<2即为f[x(2-x)]<f(
),
由f(x)在(0,+∞)上单调递减,
则
即有
,
则
<x<
.
故x的取值范围是(
,
).
可令x=y=1,则f(1)=f(1)+f(1),
即有f(1)=0;
(2)证明:由于对任意的x1,x2,当x1,x2(x1≠x2)都在(0,+∞)时,
总有(x1-x2)(f(x1)-f(x2))<0,
即x1<x2时,总有f(x1)>f(x2)成立,
则f(x)在(0,+∞)上单调递减;
(3)解:由于f(xy)=f(x)+f(y),f(
| 1 |
| 3 |
则f(
| 1 |
| 9 |
| 1 |
| 3 |
则f(x)+f(2-x)<2即为f[x(2-x)]<f(
| 1 |
| 9 |
由f(x)在(0,+∞)上单调递减,
则
|
|
则
3-2
| ||
| 3 |
3+2
| ||
| 3 |
故x的取值范围是(
3-2
| ||
| 3 |
3+2
| ||
| 3 |
点评:本题考查抽象函数及运用,考查函数的单调性及运用:解不等式,注意定义域,考查运算能力.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案
相关题目
89×90×91×92×…×100可表示为( )
A、A
| ||
B、
| ||
C、
| ||
D、
|
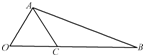 如图,∠AOB=60°,OA=2,OB=5,在线段OB上任取一点C,试求:
如图,∠AOB=60°,OA=2,OB=5,在线段OB上任取一点C,试求: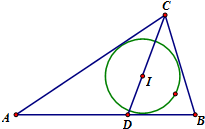 如图,△ABC中,点A(-1,0),B(1,0).圆I是△ABC的内切圆,且CI延长线交AB与点D,若
如图,△ABC中,点A(-1,0),B(1,0).圆I是△ABC的内切圆,且CI延长线交AB与点D,若