题目内容
数列{an}中,a1=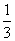 ,前n项和Sn满足Sn+1-Sn=(
,前n项和Sn满足Sn+1-Sn=(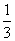 )n+1(n∈N*).
)n+1(n∈N*).
(1)求数列{an}的通项公式an以及前n项和Sn;
(2)若S1,t(S1+S2),3(S2+S3)成等差数列,求实数t的值.
解 (1)由Sn+1-Sn=(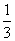 )n+1得an+1=(
)n+1得an+1=(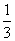 )n+1(n∈N*),
)n+1(n∈N*),
又a1=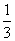 ,故an=(
,故an=(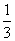 )n(n∈N*).
)n(n∈N*).
从而Sn= =
= [1-(
[1-(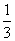 )n](n∈N*).
)n](n∈N*).
(2)由(1)可得S1=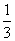 ,S2=
,S2= ,S3=
,S3= .
.
从而由S1,t(S1+S2),3(S2+S3)成等差数列得
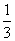 +3×(
+3×( +
+ )=2×(
)=2×(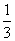 +
+ )t,解得t=2.
)t,解得t=2.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
 的取值范围是( )
的取值范围是( )
 B、
B、 C、
C、  D、
D、 
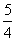 ,则数列{an}的通项公式为( )
,则数列{an}的通项公式为( )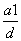 的值为( )
的值为( ) (n2-n+2)万元,乙超市第n年的销售额比前一年销售额多a
(n2-n+2)万元,乙超市第n年的销售额比前一年销售额多a n-1万元.
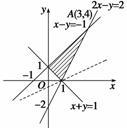
n-1万元. ,目标函数z=ax+2y仅在点(1,0)处取得最小值,则a的取值范围是( )
,目标函数z=ax+2y仅在点(1,0)处取得最小值,则a的取值范围是( )