题目内容

15．已知a＞0且a≠1，则logab＞0是（a-1）（b-1）＞0的（　　）
A．充分而不必要条件B．必要而不充分条件
C．充要条件D．既不充分也不必要条件

分析 a＞0且a≠1，则logab＞0?$\left\{\begin{array}{l}{a＞1}\\{b＞1}\end{array}\right.$，或$\left\{\begin{array}{l}{0＜a＜1}\\{0＜b＜1}\end{array}\right.$．（a-1）（b-1）＞0?$\left\{\begin{array}{l}{a＞1}\\{b＞1}\end{array}\right.$，或$\left\{\begin{array}{l}{a＜1}\\{b＜1}\end{array}\right.$．即可判断出结论．

解答 解：a＞0且a≠1，则logab＞0?$\left\{\begin{array}{l}{a＞1}\\{b＞1}\end{array}\right.$，或$\left\{\begin{array}{l}{0＜a＜1}\\{0＜b＜1}\end{array}\right.$．
（a-1）（b-1）＞0?$\left\{\begin{array}{l}{a＞1}\\{b＞1}\end{array}\right.$，或$\left\{\begin{array}{l}{a＜1}\\{b＜1}\end{array}\right.$．
故选：A．

点评 本题考查了对数函数的单调性、不等式的解法、简易逻辑的判定方法，考查了推理能力与计算能力，属于基础题．

练习册系列答案
相关题目
5．已知函数f（x）=$\frac{2lnx+{a}^{2}}{x}$+bx-2a（a∈R），其中b=${∫}_{0}^{\frac{π}{2}}$（2sin$\frac{t}{2}$•cos$\frac{t}{2}$）dt，若?x∈（1，2），使得f′（x）•x+f（x）＞0成立，则实数a的取值范围为（　　）
A．（-∞，1）B．（0，1]C．（-∞，$\frac{5}{2}$）D．（-∞，$\frac{5}{2}$]
6．若实数x，y在条件$\left\{\begin{array}{l}x+y≤4\\ x≥1\\ y≥m\end{array}\right.$下，所表示的平面区域面积为2，则$\frac{x+y+2}{x+1}$的最小值为（　　）
A．$\frac{1}{2}$B．$\frac{3}{2}$C．$\frac{2}{3}$D．2
3．高为$\sqrt{2}$的四棱锥S-ABCD的底面是边长为1的正方形，点S、A、B、C、D均同一球面上，底面ABCD的中心为O1，球心O到底面ABCD的距离为$\frac{{\sqrt{2}}}{2}$，则异面直线SO1与AB所成角的余弦值的范围为[0，$\frac{\sqrt{10}}{10}$]．
10．函数f（x）=ln|x+cosx|的图象为（　　）
A．B．C．D．
20．“干支纪年法”是中国历法上自古以来就一直使用的纪年方法．干支是天干和地支的总称．甲、乙、丙、丁、戊、已、庚、辛、壬、癸十个符号叫天干，子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥十二个符号叫地支．把干支顺序相配正好六十为一周，周而复始，循环记录，这就是俗称的“干支表”．2016年是干支纪年法中的丙申年，那么2017年是干支纪年法中的（　　）
A．丁酉年B．戊未年C．乙未年D．丁未年
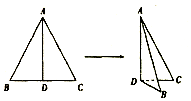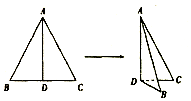7．如图，将边长为2的正△ABC沿着高AD折起，使∠BDC=60°，若折起后A、B、C、D四点都在球O的表面上，则球O的表面积为（　　）
A．$\frac{13}{2}π$B．$\frac{13}{3}π$C．$\frac{{13\sqrt{3}}}{2}π$D．$\frac{{13\sqrt{3}}}{3}π$
4．设f（x）是定义在R上的周期为3的函数，当x∈[-2，1）时，$f（x）=\left\{\begin{array}{l}4{x^2}-2，-2≤x≤0\\ x，0＜x＜1\end{array}\right.$，则$f（\frac{5}{2}）$=（　　）
A．0B．1C．$\frac{1}{2}$D．-1
5．设命题p：“?a≥-1，ln（en+1）＞$\frac{1}{2}$”，则?p为（　　）
A．?a≥-1，ln（en+1）≤$\frac{1}{2}$B．?a＜-1，ln（en+1）≤$\frac{1}{2}$C．?a≥-1，ln（en+1）≤$\frac{1}{2}$D．?a＜-1，ln（en+1）≤$\frac{1}{2}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网