题目内容
4.设f(x)是定义在R上的周期为3的函数,当x∈[-2,1)时,$f(x)=\left\{\begin{array}{l}4{x^2}-2,-2≤x≤0\\ x,0<x<1\end{array}\right.$,则$f(\frac{5}{2})$=( )| A. | 0 | B. | 1 | C. | $\frac{1}{2}$ | D. | -1 |
分析 由函数的周期性得到f($\frac{5}{2}$)=f(-$\frac{1}{2}$),由此能求出结果.
解答 解:∵f(x)是定义在R上的周期为3的函数,
当x∈[-2,1)时,$f(x)=\left\{\begin{array}{l}4{x^2}-2,-2≤x≤0\\ x,0<x<1\end{array}\right.$,
∴f($\frac{5}{2}$)=f(-$\frac{1}{2}$)=4×(-$\frac{1}{2}$)2-2=-1.
故选:D.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
15.已知a>0且a≠1,则logab>0是(a-1)(b-1)>0的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
13.已知x,y是实数,i是虚数单位,$\frac{x}{1+i}=1-yi$,则复数x+yi在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
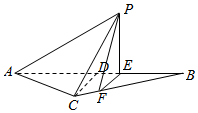 等腰△ABC的底边$AB=6\sqrt{6}$,高CD=3,点E是线段BD上异于点B,D的动点.点F在BC边上,且EF⊥AB.现沿EF将△BEF折起到△PEF的位置,使PE⊥AE.
等腰△ABC的底边$AB=6\sqrt{6}$,高CD=3,点E是线段BD上异于点B,D的动点.点F在BC边上,且EF⊥AB.现沿EF将△BEF折起到△PEF的位置,使PE⊥AE.