题目内容
12.已知定点A(4,0),P是椭圆4x2+9y2=36上的动点,则线段AP的中点的轨迹方程是4(x-2)2+9y2=9.分析 设P(m,n),即有4m2+9n2=36,AP的中点为(x,y),运用中点坐标公式,以及代入法,即可得到所求轨迹方程.
解答 解:设P(m,n),即有4m2+9n2=36,
AP的中点为(x,y),
即有2x=4+m,2y=n,
即m=2x-4,n=2y,
即有4(2x-4)2+9(2y)2=36,
即4(x-2)2+9y2=9.
故答案为:4(x-2)2+9y2=9.
点评 本题考查轨迹方程的求法,注意运用中点坐标公式和椭圆的方程,考查运算能力,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.在等腰梯形ABCD中,AB∥CD,且|AB|=2,|AD|=1,|CD|=2x,其中x∈(0,1),以A,B为焦点且过点D的双曲线的离心率为e1,以C,D为焦点且过点A的椭圆的离心率为e2,若对任意x∈(0,1)都有不等式$t<\frac{{{{({e_1}+{e_2})}^2}}}{8}$恒成立,则t的最大值为( )
| A. | $\frac{7}{4}$ | B. | $\frac{3}{8}$ | C. | $\frac{5}{8}$ | D. | $\frac{5}{4}$ |
1.如图1,已知正方体ABCD-A1B1C1D1的棱长为a,动点M、N、Q分别在线段AD1、B1C、C1D1上,当三棱锥Q-BMN的正视图如图所示时,三棱锥Q-BMN的侧视图的面积等于( )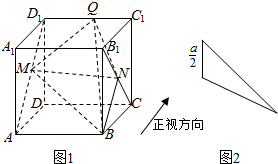

| A. | $\frac{1}{4}{a}^{2}$ | B. | $\frac{3}{4}{a}^{2}$ | C. | $\frac{1}{2}{a}^{2}$ | D. | $\frac{\sqrt{3}}{2}{a}^{2}$ |
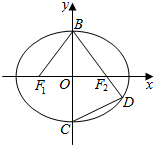 如图,在平面直角坐标系xOy中,F1,F2分别是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点,B,C分别为椭圆上、下顶点,直线BF2与椭圆的另一个交点为D,若tan∠F1BO=$\frac{3}{4}$,则直线CD的斜率为$\frac{12}{25}$.
如图,在平面直角坐标系xOy中,F1,F2分别是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点,B,C分别为椭圆上、下顶点,直线BF2与椭圆的另一个交点为D,若tan∠F1BO=$\frac{3}{4}$,则直线CD的斜率为$\frac{12}{25}$.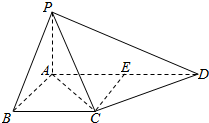 如图,在梯形ABCD中,AD∥BC,AB⊥BC,AB=BC=1,PA⊥平面ABCD,CD⊥PC,PD=2PA.
如图,在梯形ABCD中,AD∥BC,AB⊥BC,AB=BC=1,PA⊥平面ABCD,CD⊥PC,PD=2PA.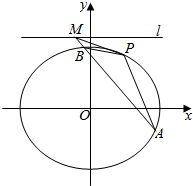 如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点P(2,3),离心率e=$\frac{1}{2}$,直线1的方程为y=4.
如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点P(2,3),离心率e=$\frac{1}{2}$,直线1的方程为y=4.