题目内容

4．用总长14.8m的钢条制作一个长方体容器的框架，若容器底面的长比宽多0.5m，要使它的容积最大，则容器底面的宽为多少？

分析 将容器容积表示成底面短边长x的函数关系，然后利用导数求此函数的最值，注意如何选择自变量．

解答 解：设容器底面短边长为x m，
则另一边长为（x+0.5）m，高为3.2-2x．
由3.2-2x＞0和x＞0，
得0＜x＜1.6，
设容器的容积为ym3，
则有y=x（x+0.5）（3.2-2x），（0＜x＜1.6）．
整理，得y=-2x3+2.2x2+1.6x，
∴y′=-6x2+4.4x+1.6．--6分
令 y′=0，有x=1．
从而在定义域（0，1.6）内只有在x=1 处使y取最大值，
这时，长x+0.5=1.5m，宽x=1m，
故容器底面的宽为1米．--12分

点评 本小题主要考查应用所学导数的知识、思想和方法解决实际问题的能力，建立函数式、解方程、不等式、最大值等基础知识．

练习册系列答案
相关题目
14．函数y=lnx-x的单调递减区间是（　　）
A．（1，+∞）B．（0，1）C．（0，1），（-∞，0）D．（1，+∞），（-∞，0）
15．已知：平行四边形ABCD，对角线AC，BD交于点O，点E为线段OB中点，完成下列各题（用于填空的向量为图中已有有向线段所表示向量）．
（1）当以{$\overrightarrow{AB}$，$\overrightarrow{AD}$}为基底时，设$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{AD}$=$\overrightarrow{b}$，
用$\overrightarrow{a}$，$\overrightarrow{b}$表示$\overrightarrow{OD}$=$\frac{1}{2}（\overrightarrow{b}-\overrightarrow{a}）$；
用$\overrightarrow{a}$，$\overrightarrow{b}$表示$\overrightarrow{AE}$=$\frac{3}{4}\overrightarrow{a}+\frac{1}{4}\overrightarrow{b}$；
（2）设点MN分别为边DC，BC中点．
①当以{$\overrightarrow{AB}$，$\overrightarrow{AD}$}为基底时，设$\overrightarrow{AB}$=$\overrightarrow{c}$，$\overrightarrow{AD}$=$\overrightarrow{d}$，
用$\overrightarrow{c}$，$\overrightarrow{d}$表示$\overrightarrow{AN}$，则$\overrightarrow{AN}$=$\overrightarrow{c}$+$\frac{1}{2}\overrightarrow{d}$．
②当以{$\overrightarrow{AM}$，$\overrightarrow{AN}$}为基底时，设$\overrightarrow{AM}$=$\overrightarrow{m}$，$\overrightarrow{AN}$=$\overrightarrow{n}$，用$\overrightarrow{m}$，$\overrightarrow{n}$表示：
$\overrightarrow{AB}$=$\frac{4}{3}\overrightarrow{n}-\frac{2}{3}\overrightarrow{m}$，$\overrightarrow{AC}$=$\frac{2}{3}\overrightarrow{n}+\frac{2}{3}\overrightarrow{m}$，$\overline{OE}$=$\frac{1}{2}\overrightarrow{n}+\frac{1}{2}\overrightarrow{m}$．
12．已知二阶矩阵M有特征值λ=8及对应的一个特征向量$\overrightarrow{e_1}=[\begin{array}{l}1\\ 1\end{array}]$，并且矩阵M将点（-1，3）变换为（0，8）．求矩阵M．
19．若$\overrightarrow{AB}•\overrightarrow{BC}=0$，$|{\overrightarrow{AB}}|=1$，$|{\overrightarrow{BC}}|=2$，$\overrightarrow{AD}•\overrightarrow{DC}=0$，则$|{\overrightarrow{BD}}|$的最大值为$\sqrt{5}$．
9．一个几何体的三视图如图所示，则该几何体的表面积为（　　）
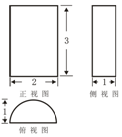
A．4πB．5π+6C．3π+6D．4π+6
16．曲线$y={x^3}-\sqrt{3}x+2$上的任意一点P处切线的倾斜角的取值范围是（　　）
A．$[{0，\frac{π}{2}}）∪[{\frac{2π}{3}，π}）$B．$[{\frac{2π}{3}，π}）$C．$[{0，\frac{π}{2}}）∪[{\frac{5π}{6}，π}）$D．$[{\frac{5π}{6}，π}）$
13．已知函数f（x）=x2+x，若f（x-2）+f（x）＜0成立，则x取值范围是∅．
14．直线y=kx+1-k与椭圆$\frac{x^2}{9}+\frac{y^2}{4}=1$的位置关系为（　　）
A．相交B．相切C．相离D．不确定

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网