题目内容
19．若$\overrightarrow{AB}•\overrightarrow{BC}=0$，$|{\overrightarrow{AB}}|=1$，$|{\overrightarrow{BC}}|=2$，$\overrightarrow{AD}•\overrightarrow{DC}=0$，则$|{\overrightarrow{BD}}|$的最大值为$\sqrt{5}$．分析 根据题意可得AB⊥BC，AD⊥DC．因此四边形ABCD内接于圆O．可得|$\overrightarrow{BD}$|的最大值为直径AC
解答 
解：如图所示：∵$\overrightarrow{AB}•\overrightarrow{BC}=0$，$\overrightarrow{AD}•\overrightarrow{DC}=0$，
∴$\overrightarrow{AB}$⊥$\overrightarrow{BC}$，$\overrightarrow{AD}$⊥$\overrightarrow{DC}$，
∴四边形ABCD内接于圆O．
可得⊙O的直径AC=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$．
则|$\overrightarrow{BD}$|的最大值为直径$\sqrt{5}$．
故答案为：$\sqrt{5}$
点评 本题考查了圆的内接四边形、数量积运算性质，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
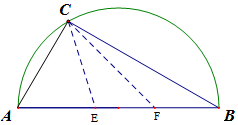如图，有一直径为8米的半圆形空地，现计划种植果树，但需要有辅助光照．半圆周上的C处恰有一可旋转光源满足果树生长的需要，该光源照射范围是$∠ECF=\frac{π}{6}$，点E，F在直径AB上，且$∠ABC=\frac{π}{6}$．