题目内容
16.曲线$y={x^3}-\sqrt{3}x+2$上的任意一点P处切线的倾斜角的取值范围是( )| A. | $[{0,\frac{π}{2}})∪[{\frac{2π}{3},π})$ | B. | $[{\frac{2π}{3},π})$ | C. | $[{0,\frac{π}{2}})∪[{\frac{5π}{6},π})$ | D. | $[{\frac{5π}{6},π})$ |
分析 设P(m,n),求出函数y的导数,求得切线的斜率,由二次函数的性质可得斜率的范围,再由直线的斜率公式k=tanα(0≤α<π且α≠$\frac{π}{2}$),即可得到所求范围.
解答 解:设P(m,n),
y=x3-$\sqrt{3}$x+2的导数为y′=3x2-$\sqrt{3}$,
即有切线的斜率为k=3m2-$\sqrt{3}$,
由直线的斜率公式k=tanα(0≤α<π,且α≠$\frac{π}{2}$),
可得tanα≥-$\sqrt{3}$,
解得α∈$[{0,\frac{π}{2}})∪[{\frac{2π}{3},π})$,
故选A.
点评 本题考查导数的运用:求切线的斜率,考查导数的几何意义,以及直线的斜率公式和倾斜角的范围,属于中档题.

练习册系列答案
相关题目
6.已知点 A(-4,0),B(4,0),C(0,4),直线y=ax+b(a>0)将△ABC分割为面积相等的两部分,则 b的取值范围是( )
| A. | $({0,4-2\sqrt{2}})$ | B. | $({4-2\sqrt{2},2})$ | C. | $({4-2\sqrt{2},\frac{4}{3}}]$ | D. | $({\frac{4}{3},2}]$ |
5.下列函数中为偶函数的是( )
| A. | y=sin|x| | B. | y=sin2x | C. | y=-sinx | D. | y=sinx+1 |
6.中央电视台第一套节目午间新闻的播出时间是每天中午12:00到12:30,在某星期天中午的午间新闻中将随机安排播出时长5分钟的有关电信诈骗的新闻报道.若小张于当天12:20打开电视,则他能收看到这条新闻的完整报道的概率是( )
| A. | $\frac{2}{5}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{6}$ |
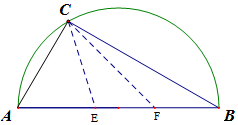 如图,有一直径为8米的半圆形空地,现计划种植果树,但需要有辅助光照.半圆周上的C处恰有一可旋转光源满足果树生长的需要,该光源照射范围是$∠ECF=\frac{π}{6}$,点E,F在直径AB上,且$∠ABC=\frac{π}{6}$.
如图,有一直径为8米的半圆形空地,现计划种植果树,但需要有辅助光照.半圆周上的C处恰有一可旋转光源满足果树生长的需要,该光源照射范围是$∠ECF=\frac{π}{6}$,点E,F在直径AB上,且$∠ABC=\frac{π}{6}$.