题目内容
从椭圆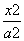 +
+ =1(a>b>0)上一点P向x轴作垂线,垂足恰为左焦点F1,A是椭圆与x轴正半轴的交点,B是椭圆与y轴正半轴的交点,且AB∥OP(O是坐标原点),则该椭圆的离心率是( )
=1(a>b>0)上一点P向x轴作垂线,垂足恰为左焦点F1,A是椭圆与x轴正半轴的交点,B是椭圆与y轴正半轴的交点,且AB∥OP(O是坐标原点),则该椭圆的离心率是( )
A.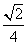 B.
B.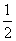
C.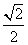 D.
D.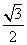
C
[解析] 本题考查了椭圆离心率的求法.
根据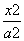 +
+ =1可得F1(-c,0),P(-c,
=1可得F1(-c,0),P(-c, ),故OP与AB的斜率分别是kOP=-
),故OP与AB的斜率分别是kOP=- ,kAB=-
,kAB=- ,根据OP∥AB得-
,根据OP∥AB得- =-
=- ,即b=c.
,即b=c.
由于a2=b2+c2,即a2=2c2,故e= =
=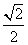 .
.

练习册系列答案
相关题目

 在
在 时有极值
时有极值 ,求
,求 的值;
的值; 的图象与函数
的图象与函数 的图象恰有三个不同的交点,求实数
的图象恰有三个不同的交点,求实数 的取值范围.
的取值范围.
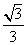 B.
B.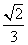
 ,则C的离心率e=________.
,则C的离心率e=________. B.
B.
 D.
D.
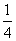 B.±
B.±
 D.无法求解
D.无法求解