题目内容
已知椭圆C: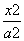 +
+ =1(a>b>0)的左焦点为F,C与过原点的直线相交于A,B两点,连接AF,BF.若|AB|=10,|AF|=6,cos∠ABF=
=1(a>b>0)的左焦点为F,C与过原点的直线相交于A,B两点,连接AF,BF.若|AB|=10,|AF|=6,cos∠ABF= ,则C的离心率e=________.
,则C的离心率e=________.

[解析] 本题考查椭圆的几何性质,解三角形问题.
在△ABF中,由余弦定理得,
cos∠ABF= ,
,
∴|BF|2-16|BF|+64=0,∴|BF|=8.
设右焦点为F1,因为直线过原点,∴|BF1|=|AF|=6,
∴2a=|BF|+|BF1|=14,∴a=7,
∵O为Rt△ABF斜边AB的中点,
∴|OF|=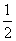 |AB|=5,∴c=5,∴e=
|AB|=5,∴c=5,∴e= .
.

练习册系列答案
相关题目
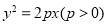 的焦点
的焦点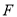 恰好是双曲线
恰好是双曲线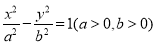 的右焦点,且两条曲线的交点的连线过点
的右焦点,且两条曲线的交点的连线过点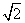 =0 B.x+y+1=0
=0 B.x+y+1=0 +
+ =1 B.
=1 B.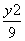 =1
=1 =1 D.
=1 D.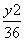 =1
=1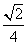 B.
B.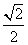 D.
D.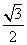
 ,则λ等于( )
,则λ等于( ) D.2或-
D.2或-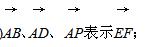
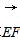 的模.
的模.