题目内容
已知函数
若 在
在 时有极值
时有极值 ,求
,求 的值;
的值;
(2)在(1)的条件下,若函数 的图象与函数
的图象与函数 的图象恰有三个不同的交点,求实数
的图象恰有三个不同的交点,求实数 的取值范围.
的取值范围.
(1) ;(2)
;(2) .
.
【解析】
试题分析:(1)根据 在
在 取得极值,得到
取得极值,得到 解得
解得 的值;(2)利用(1)中得到函数的解析式,对其求导,进而找到其单调性和极值,结合图像,可得到
的值;(2)利用(1)中得到函数的解析式,对其求导,进而找到其单调性和极值,结合图像,可得到 的取值范围.
的取值范围.
试题解析:(1) 
由已知得  解得:
解得:  经验证,符合题意.
经验证,符合题意.
(2)由(1)知 
由 得
得 
列表如下:
|
|
|
|
|
|
| + | 0 | — | 0 | + |
| 单调递增 | 极大值 | 单调递减 | 极小值 | 单调递增 |
根据表格,当 时函数取得极大值,且极大值为
时函数取得极大值,且极大值为 ,当
,当 时函数取得极小值,且极小值为
时函数取得极小值,且极小值为 ,所以根据题意可知
,所以根据题意可知 
所以  的取值范围是:
的取值范围是: .
.
考点:1.函数的极值;2.函数求导;3.函数的零点个数.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目








 的半径为1,圆心在第一象限,且与直线
的半径为1,圆心在第一象限,且与直线 和
和 轴都相切,则该圆的标准方程是 .
轴都相切,则该圆的标准方程是 .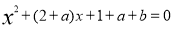 的两根是
的两根是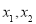 ,且
,且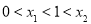 ,则
,则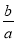 的取值范围是( )
的取值范围是( )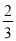 ) B、[-2,-
) B、[-2,- 的等比中项是( )
的等比中项是( ) C、
C、 D、以上选项都不对
D、以上选项都不对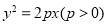 的焦点
的焦点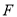 恰好是双曲线
恰好是双曲线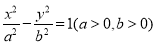 的右焦点,且两条曲线的交点的连线过点
的右焦点,且两条曲线的交点的连线过点
 D.2
D.2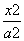 +
+ =1(a>b>0)上一点P向x轴作垂线,垂足恰为左焦点F1,A是椭圆与x轴正半轴的交点,B是椭圆与y轴正半轴的交点,且AB∥OP(O是坐标原点),则该椭圆的离心率是( )
=1(a>b>0)上一点P向x轴作垂线,垂足恰为左焦点F1,A是椭圆与x轴正半轴的交点,B是椭圆与y轴正半轴的交点,且AB∥OP(O是坐标原点),则该椭圆的离心率是( )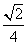 B.
B.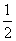
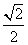 D.
D.