题目内容
1.今年“五一”期间,某公园举行免费游园活动,免费开放一天,早晨6时30分有2人进入公园,接下来的第一个30分钟内有4人进去1人出来,第二个30分钟内有8人进去2人出来,第三个30分钟内有16人进去3人出来,第四个30分钟内有32人进去4人出来…按照这种规律进行下去,到上午11时公园内的人数是( )| A. | 212-57 | B. | 211-47 | C. | 210-38 | D. | 29-30 |
分析 先设每个30分钟进去的人数构成数列{an},确定求数列{an}的通项公式,由于从早晨6时30分到上午11时,共有10个30分钟,故需求数列{an}的前10项和,再由等比数列前n项和公式即可得上午11时园内的人数.
解答 解:设每个30分钟进去的人数构成数列{an},则
a1=2=2-0,a2=4-1,a3=8-2,a4=16-3,a5=32-4,…,an=2n-(n-1)
设数列{an}的前n项和为Sn,依题意,
只需求S10=(2-0)+(22-1)+(23-2)+…+(210-9)=(2+22+23+…+210)-(1+2+…+9)=211-47
故选B.
点评 本题考查数列的通项公式,等比数列的前n项和公式,考查将实际问题转化为数学问题,运用数学知识解决问题的能力,属于中档题.

练习册系列答案
相关题目
16.在各项为正实数的等差数列{an}中,其前2016项的和S2016=1008,则$\frac{1}{{{a_{1001}}}}+\frac{9}{{{a_{1016}}}}$的最小值为( )
| A. | 12 | B. | 16 | C. | $\frac{1}{84}$ | D. | $\frac{2}{251}$ |
6.若函数f(x)=|x2-k|的图象与函数g(x)=x-3的图象至多一个公共点,则实数k的取值范围是( )
| A. | (-∞,3] | B. | [9,+∞) | C. | (-∞,9] | D. | (-∞,9) |
11.若直线l的一个方向向量$\overrightarrow a=(2,2,-2)$,平面α的一个法向量为$\overrightarrow b=(1,1,-1)$,则( )
| A. | l∥α | B. | l⊥α | C. | l?α | D. | A、C都有可能 |
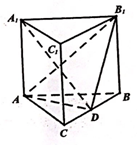 如图,已知在直三棱柱ABC-A1B1C1中,AB=AA1=2,二面角A-C1C-B的大小为$\frac{π}{3}$,点D线段BC的中点.
如图,已知在直三棱柱ABC-A1B1C1中,AB=AA1=2,二面角A-C1C-B的大小为$\frac{π}{3}$,点D线段BC的中点.