题目内容
7.在各项均为正数的等比数列{an}中,若a5a6=9,则log3a1+log3a2+…+log3a10=( )| A. | 12 | B. | 2+log35 | C. | 8 | D. | 10 |
分析 根据等比数列的性质:a1a10=a2a9=…=a5a6=9,再利用对数的运算性质即可得出.
解答 解:根据等比数列的性质:a1a10=a2a9=…=a5a6=9,
∴log3a1+log3a2+…+log3a10=log3(a1a2•…•a10)=$lo{g}_{3}({a}_{5}{a}_{6})^{5}$=$lo{g}_{3}{3}^{10}$=10,
故选:D.
点评 本题考查了等比数列的性质、对数的运算性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
18.已知直线x+ay=a+2(a∈R)与圆x2+y2-2x-2y-7=0交于M,N两点,则线段MN的长的最小值为( )
| A. | $4\sqrt{2}$ | B. | $2\sqrt{2}$ | C. | 2 | D. | $\sqrt{2}$ |
15.边长为a的正四面体的外接球半径为( )
| A. | $\frac{{\sqrt{6}}}{3}a$ | B. | $\frac{{\sqrt{6}}}{4}a$ | C. | $\frac{{\sqrt{6}}}{12}a$ | D. | $\frac{{\sqrt{3}}}{2}a$ |
2.若$\overrightarrow a=(1,1,k)$,$\overrightarrow b=(2,-1,1)$,$\overrightarrow a$与$\overrightarrow b$的夹角为60°,则k的值为( )
| A. | 0或-2 | B. | 0或2 | C. | -2 | D. | 2 |
12.设z=$\frac{2}{1-i}$+i,则|z|为( )
| A. | 1+2i | B. | 1 | C. | $\sqrt{13}$ | D. | $\sqrt{5}$ |
16.“$α=\frac{π}{6}$”是“$sinα=\frac{1}{2}$”的( )条件.
| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充要 | D. | 既不充分也不必要 |
17.若方程x2+y2+x-y+m2=0表示圆,则实数m的取值范围是( )
| A. | $m<\frac{{\sqrt{2}}}{2}$ | B. | $-\frac{{\sqrt{2}}}{2}<m<\frac{{\sqrt{2}}}{2}$ | C. | $m<-\frac{{\sqrt{2}}}{2}$ | D. | $m>\frac{{\sqrt{2}}}{2}$ |
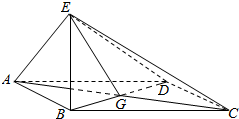 如图四棱锥E-ABCD,底面四边形ABCD为菱形,G为AC与BD的交点,BE⊥平面ABCD.
如图四棱锥E-ABCD,底面四边形ABCD为菱形,G为AC与BD的交点,BE⊥平面ABCD.