题目内容
17.若方程x2+y2+x-y+m2=0表示圆,则实数m的取值范围是( )| A. | $m<\frac{{\sqrt{2}}}{2}$ | B. | $-\frac{{\sqrt{2}}}{2}<m<\frac{{\sqrt{2}}}{2}$ | C. | $m<-\frac{{\sqrt{2}}}{2}$ | D. | $m>\frac{{\sqrt{2}}}{2}$ |
分析 由二元二次方程表示圆的条件得到m的不等式,解不等式即可得到结果.
解答 解:方程x2+y2+x-y+m2=0表示一个圆,
则1+1-4m2>0,
∴$-\frac{{\sqrt{2}}}{2}<m<\frac{{\sqrt{2}}}{2}$.
故选:B.
点评 本题考查二元二次方程表示圆的条件,属基础知识的考查,本题解题的关键是看清楚所表示的二元二次方程的各个系数之间的关系.

练习册系列答案
相关题目
7.在各项均为正数的等比数列{an}中,若a5a6=9,则log3a1+log3a2+…+log3a10=( )
| A. | 12 | B. | 2+log35 | C. | 8 | D. | 10 |
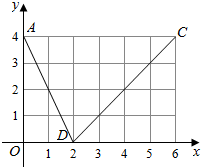 如图,函数f(x)的图象是折线段ABC,其中点A,B,C的坐标分别为(0,4),(2,0),(6,4),则f{f[f(2)]}=( )
如图,函数f(x)的图象是折线段ABC,其中点A,B,C的坐标分别为(0,4),(2,0),(6,4),则f{f[f(2)]}=( )