题目内容
20.已知函数f(x)是周期为2的奇函数,当x∈[0,1)时,f(x)=lg(x+1),则$f(\frac{2016}{5})+lg18$=( )| A. | 1 | B. | 2 | C. | 5 | D. | 10 |
分析 由已知中函数f(x)是周期为2的奇函数,可得$f(\frac{2016}{5})$=$f(-\frac{4}{5})$=-$f(\frac{4}{5})$,进而结合对数的运算性质,可得答案.
解答 解:∵当x∈[0,1)时,f(x)=lg(x+1),
$f(\frac{4}{5})$=lg$\frac{9}{5}$
又∵函数f(x)是周期为2的奇函数,
∴$f(\frac{2016}{5})$=$f(-\frac{4}{5})$=-$f(\frac{4}{5})$=-lg$\frac{9}{5}$,
∴$f(\frac{2016}{5})+lg18$=lg18-lg$\frac{9}{5}$=1g10=1,
故选:A.
点评 本题考查的知识点是函数的周期性,函数的奇偶性,函数求值,对数的运算性质,难度中档.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
11.设函数$f(x)=\left\{\begin{array}{l}x,0≤x<1\\ \frac{1}{{f({x+1})}}-1,-1<x<0\end{array}\right.$,g(x)=f(x)-4mx-m,其中m≠0.若函数g(x)在区间(-1,1)上有且仅有一个零点,则实数m的取值范围是( )
| A. | $m≥\frac{1}{4}$或m=-1 | B. | $m≥\frac{1}{4}$ | C. | $m≥\frac{1}{5}$或m=-1 | D. | $m≥\frac{1}{5}$ |
5.执行如图的程序框图,则输出S的值为( )


| A. | 2 | B. | -3 | C. | $-\frac{1}{2}$ | D. | $\frac{1}{3}$ |
12.已知等差数列{an}的前n项和为Sn,a9=1,S18=0,当Sn取最大值时n的值为( )
| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
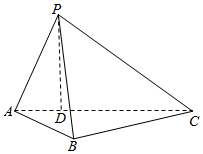 如图所示,在三棱锥P-ABC中,$AB=BC=2\sqrt{3}$,平面PAC⊥平面ABC,PD⊥AC于点D,AD=2,CD=4,PD=3.
如图所示,在三棱锥P-ABC中,$AB=BC=2\sqrt{3}$,平面PAC⊥平面ABC,PD⊥AC于点D,AD=2,CD=4,PD=3.