题目内容
9.已知数列{an}的通项公式是${a_n}=\frac{1}{{{{(n+1)}^2}}}$,(n∈N*),记bn=(1-a1)(1-a2)…(1-an)(1)写出数列{bn}的前三项;
(2)猜想数列{bn}通项公式,并用数学归纳法加以证明.
分析 (1)由题意可得,代值计算即可,
(2)猜想,检验n=1时等式成立,假设n=k时命题成立,证明当n=k+1时命题也成立.
解答 解:(1)${b_1}=\frac{3}{4}$,${b_2}=\frac{4}{6}$,${b_3}=\frac{5}{8}$
(2)猜想:${b_n}=\frac{n+2}{2(n+1)}$
①n=1时,${b_1}=\frac{1+2}{4}=\frac{3}{4}$
②假设n=k时,${b_k}=\frac{k+2}{2(k+1)}$
当n=k+1时bk+1=(1-a1)(1-a2)…(1-ak)(1-ak+1)
=bk(1-ak+1)=$\frac{k+2}{2(k+1)}$(1-$\frac{1}{(k+2)^{2}}$)
=$\frac{k+2}{2(k+1)}$•$\frac{{k}^{2}+4k+3}{(k+2)^{2}}$=$\frac{(k+2)(k+1)(k+3)}{2(k+1)(k+2)^{2}}$=$\frac{k+3}{2(k+2)}$
综合①②:${b_n}=\frac{n+2}{2(n+1)}$.
点评 本题考查数列的递推公式,用数学归纳法证明等式成立.证明当n=k+1时命题也成立,是解题的难点.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
19.在空间直角坐标系O-xyz中,点(1,2,-2)关于点(-1,0,1)的对称点是( )
| A. | (-3,-2,4) | B. | (3,-2,-4) | C. | (-3,2,-4) | D. | (-3,2,4) |
20.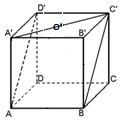 如图所示,正方体ABCD-A'B'C'D'的棱长为1,点O是正方形A'B'C'D'的中心,则点O到平面ABC'D'的距离是( )
如图所示,正方体ABCD-A'B'C'D'的棱长为1,点O是正方形A'B'C'D'的中心,则点O到平面ABC'D'的距离是( )
 如图所示,正方体ABCD-A'B'C'D'的棱长为1,点O是正方形A'B'C'D'的中心,则点O到平面ABC'D'的距离是( )
如图所示,正方体ABCD-A'B'C'D'的棱长为1,点O是正方形A'B'C'D'的中心,则点O到平面ABC'D'的距离是( )| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{\sqrt{2}}{4}$ |
4.若函数f(x)=e-x+ax,x∈R有两个零点,则实数a的取值范围为( )
| A. | 1<a<e | B. | a>e | C. | -e<a<-1 | D. | a<-e |
14.银川一中最强大脑社对高中学生的记忆力x和判断力y进行统计分析,得表数据
(1)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$
(2)试根据已求出的线性回归方程,预测记忆力为9的同学的判断力.
参考公式:$\left\{{\begin{array}{l}{\hat b=\frac{{\sum_{i=1}^n{({x_i}-\bar x)({y_i}-\bar y)}}}{{\sum_{i=1}^n{{{({x_i}-\bar x)}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\bar x\bar y}}}{{\sum_{i=1}^n{{x_i}^2-n{{\bar x}^2}}}}}\\{\hat a=\bar y-\hat b\bar x}\end{array}}\right.$.
| x | 6 | 8 | 10 | 12 |
| y | 2 | 3 | 5 | 6 |
(2)试根据已求出的线性回归方程,预测记忆力为9的同学的判断力.
参考公式:$\left\{{\begin{array}{l}{\hat b=\frac{{\sum_{i=1}^n{({x_i}-\bar x)({y_i}-\bar y)}}}{{\sum_{i=1}^n{{{({x_i}-\bar x)}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\bar x\bar y}}}{{\sum_{i=1}^n{{x_i}^2-n{{\bar x}^2}}}}}\\{\hat a=\bar y-\hat b\bar x}\end{array}}\right.$.
9.已知P是ABC所在平面内一点,$\overrightarrow{PB}$+$\overrightarrow{PC}$+$\frac{3}{5}$$\overrightarrow{PA}$=$\overrightarrow{0}$,现将一粒黄豆随机撒在ABC内,则黄豆落在PBC内的概率是( )
| A. | $\frac{3}{13}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{10}$ | D. | $\frac{10}{13}$ |