题目内容
17.设定义在R上的可导函数f(x)的导函数为f′(x),若f(3)=1,且3f(x)+xf′(x)>1,则不等式(x-2017)3f(x-2017)-27>0的解集为( )| A. | (2014,+∞) | B. | (0,2014) | C. | (0,2020) | D. | (2020,+∞) |
分析 令g(x)=x3f(x),判断出g(x)在(0,+∞)递增,原不等式转化为g(x-2017)>g(3),解出即可.
解答 解:∵3f(x)+xf′(x)>1,
∴3x2f(x)+x3f′(x)>x2>0,
故[x3f(x)]′>0,
故g(x)=x3f(x)在(0,+∞)递增,
∵(x-2017)3f(x-2017)-27f(3)>0,
∴(x-2017)3f(x-2017)>33f(3),
即g(x-2017)>g(3),故x-2017>3,解得:x>2020,
故原不等式的解集是(2020,+∞),
故选:D.
点评 本题考查了函数与导数,考查不等式的解集以及不等式恒成立问题,考查转化思想以及运算求解能力,是一道中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.食品添加剂会引起血脂增高、血压增高、血糖增高等疾病,为了解三高疾病是否与性别有关,医院随机对入院的60人进行了问卷调查,得到了如下的列联表:
(1)请将列联表补充完整;
(2)为了研究三高疾病是否与性别有关,请计算出统计量K2,并说明你有多大把握认为患三高疾病与性别有关.
下列的临界值表供参考:
(参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$)
(1)请将列联表补充完整;
| 患三高疾病 | 不患三高疾病 | 合计 | |
| 男 | 24 | 6 | 30 |
| 女 | 12 | 18 | 30 |
| 合计 | 36 | 24 | 60 |
下列的临界值表供参考:
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
5.设函数f(x)=log2x,在区间(0,5)上随机取一个数x,则f(x)<2的概率为( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
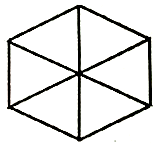 用四种不同的颜色为正六边形(如图)中的六块区域涂色,要求有公共边的区域涂不同颜色,一共有732种不同的涂色方法.
用四种不同的颜色为正六边形(如图)中的六块区域涂色,要求有公共边的区域涂不同颜色,一共有732种不同的涂色方法. 在斜三棱柱ABC-A1B1C1中,侧面AC1⊥平面ABC,$A{A_1}=\sqrt{2}a$,A1C=CA=AB=a,AB⊥AC,D是AA1的中点.
在斜三棱柱ABC-A1B1C1中,侧面AC1⊥平面ABC,$A{A_1}=\sqrt{2}a$,A1C=CA=AB=a,AB⊥AC,D是AA1的中点.