题目内容
已知f(α)=
.
(1)化简f(α);
(2)若f(α)=
,且
<α<
,求cosα-sinα的值;
(3)若α=-
,求f(α)的值.
| sin2(π-α)•cos(2π-α)•tan(-π+α) |
| sin(-π+α)•tan(-α+3π) |
(1)化简f(α);
(2)若f(α)=
| 1 |
| 8 |
| π |
| 4 |
| π |
| 2 |
(3)若α=-
| 47π |
| 4 |
考点:运用诱导公式化简求值
专题:三角函数的求值
分析:(1)利用诱导公式对f(α)=
化简即可;
(2)结合(1)知f(α)=
sin2α=
,可求得sin2α=
,cosα-sinα<0,对所求关系式平方后再开方即可;
(3)将α=-
,代入f(α)=
sin2α即可.
| sin2(π-α)•cos(2π-α)•tan(-π+α) |
| sin(-π+α)•tan(-α+3π) |
(2)结合(1)知f(α)=
| 1 |
| 2 |
| 1 |
| 8 |
| 1 |
| 4 |
(3)将α=-
| 47π |
| 4 |
| 1 |
| 2 |
解答:
解:(1)f(α)=
=sinαcosα=
sin2α;
(2)∵f(α)=
sin2α=
,∴sin2α=
,
又
<α<
,∴cosα-sinα<0,
∵(cosα-sinα)2=1-sin2α=
,
∴cosα-sinα=-
;
(3)∵α=-
,
∴2α=-
=-24π+
,
∴f(α)=
sin2α=
.
| sin2αcosαtanα |
| -sinα•(-tanα) |
| 1 |
| 2 |
(2)∵f(α)=
| 1 |
| 2 |
| 1 |
| 8 |
| 1 |
| 4 |
又
| π |
| 4 |
| π |
| 2 |
∵(cosα-sinα)2=1-sin2α=
| 3 |
| 4 |
∴cosα-sinα=-
| ||
| 2 |
(3)∵α=-
| 47π |
| 4 |
∴2α=-
| 47π |
| 2 |
| π |
| 2 |
∴f(α)=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查三角函数的化简求值,着重考查诱导公式的应用,考查二倍角的正弦及同角三角函数间的关系式的应用,属于中档题.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
已知集合A={0,2,4,6},B={2,4,8,16},则A∩B等于( )
| A、{2} |
| B、{4} |
| C、{0,2,4,6,8,16} |
| D、{2,4} |
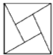 如图,大正方形的面积是13,四个全等的直角三角形围成一个小正方形,直角三角形的较短边长为2,向大正方形内投一飞镖,则飞镖落在小正方形内的概率为
如图,大正方形的面积是13,四个全等的直角三角形围成一个小正方形,直角三角形的较短边长为2,向大正方形内投一飞镖,则飞镖落在小正方形内的概率为