题目内容
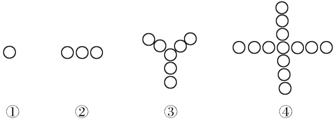
如图①②③④所示,它们都是由小圆圈组成的图案.现按同样的排列规则进行排列,记第n个图形包含的小圆圈个数为f(n),则
(Ⅰ)f(5)= ;
(Ⅱ)f(2014)的个位数字为 .

(Ⅰ)f(5)=
(Ⅱ)f(2014)的个位数字为
考点:归纳推理
专题:规律型
分析:设第n个图案的点的个数为f(n),可得f(n)-f(n-1)=2(n-1),n-1个式子相加,由等差数列的求和公式可得结果.
解答:
解:设第n个图案的点的个数为an,由题意可得f(1)=1,f(2)=3,f(3)=7,f(4)=13,
故f(2)-f(1)=2,f(3)-f(2)=4,f(4)-f(3)=6,…,
由此可推得f(n)-f(n-1)=2(n-1),以上n-1个式子相加可得:
f(2)-f(1)+f(3)-f(2)+f(4)-f(3)+…+f(n)-f(n-1)=2+4+6+…+2(n-1),
化简可得f(n)-1=
=n(n-1),故f(n)=n(n-1)+1,
(I)当n=5时,
f(5)=5×4+1=21,
(II)当n=2014时,
f(2014)=2014×2013+1,
个位数为3,
故答案为:(Ⅰ)21;(Ⅱ)3
故f(2)-f(1)=2,f(3)-f(2)=4,f(4)-f(3)=6,…,
由此可推得f(n)-f(n-1)=2(n-1),以上n-1个式子相加可得:
f(2)-f(1)+f(3)-f(2)+f(4)-f(3)+…+f(n)-f(n-1)=2+4+6+…+2(n-1),
化简可得f(n)-1=
| (n-1)(2+2n-2) |
| 2 |
(I)当n=5时,
f(5)=5×4+1=21,
(II)当n=2014时,
f(2014)=2014×2013+1,
个位数为3,
故答案为:(Ⅰ)21;(Ⅱ)3
点评:本题考查归纳推理,构造数列并得出数列的特点是解决问题的关键,属基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目